Predicting The Discharge Trajectory From Belt Conveyors
P.C. Arnold & G.L. Hill
Acknowledgements : The Bionic Research Institute, Chute Design Conference 1991
There are several methods available to the chute designer for predicting product trajectories. This paper reviews alternative methods and recommends the most appropriate ones.
Professor P .C. Arnold of the University of Wollongong, NSW, Australia, is the author of numerous technical papers in the field of powder and bulk solids handling.
This paper on trajectory formulae is pivotal to proper chute design. Professor Arnold gave permission to reprint the paper as his contribution to this Conference.
SUMMARY
There are several methods available to the engineer for making trajectory predictions of the path followed by a bulk solid discharge from a belt conveyor. Some of the methods include the M.H.E.A [1] Handbook of Recommended Practice for Belt Conveyors, Booth [2] and Korzen [3], while a fourth method is presented in the Dunlop Conveyor Manual [4]. This paper contrasts and compares the various methods, with the emphasis being placed on the Dunlop/Booth as a simpler way of obtaining a more correct solution to the discharge trajectory of a 'free flowing' bulk solid. While the techniques described by Korzen are useful if the material possess high amounts of adhesion or if air drag is a factor.
1. INTRODUCTION
Engineers and designers use plots of material trajectories from belt conveyors to aid in the placement and design of transfer chutes, impacts plates, and receiving bins. Thus the trajectory of the discharged material must be predicted as accurately as possible. To do this they may turn to in-house technical specifications, consult the various publications available on the subject such as put out the C.E.M.A. [5] or M.H.E.A. ore rely on a catalogue like the Dunlop Conveyor Manual to predict a discharge trajectory.
With all the above methods available and nearly all of them providing different approaches, it could become confusing to a designer as to which method best suits his application. Some methods such as that described in the Dunlop Conveyor Manual are simple and quick to understand relying on a graphical format for presenting data on slow moving conveyors and a more traditional ballistics approach for faster belt speeds. Although quick and easy to implement the Dunlop method has limited accuracy for slow conveyors and neglects to mention how to plot the outer edge of the material stream.
Other methods like those detailed in the C.E.M.A handbook are slightly more tedious and difficult to follow but account for almost all standard combinations of belt width, troughing idlers and bulk material characteristics, though frictional effects and adhesion are deregarded.
There are also two other methods worth noting those of Booth and Korzen Booth supplies an analytical as well as a graphical approach that gives similar results to the Dunlop method. The techniques described by Korzen provide the most thorough and detailed analytical methods of all the choices available for predicting material trajectories.
2. PREDICTING MATERIAL TRAJECTORY
Following is a review of some of the more common techniques used to predict the flight path of a bulk solid discharged from a belt conveyor. Included in this discussion are some variations on these methods.
2.1 C.E.M.A.
The C.E.M.A. addresses five points in its determination of a material trajectory, briefly these are:
i) Center of Mass
This is taken as the center of gravity of the load shape cross-section at the point where the moving conveyor belt becomes tangent to the pulley.ii) Velocities
The material and the belt are moving at the same linear velocity up to the point where the belt becomes tangent to the pulley. At this point the material begins to accelerate up to the tangential velocity based on the center of mass from the pulley center.iii) Start of Trajectory
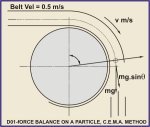
The trajectory starts at the point where the radial and centrifugal forces acting on the center of mass balance each other. Fig. 1 illustrates this point for a slow moving conveyor where the material has wrapped 84 around the pulley before falling off.
Fig. 1: Force balance on a particle, C.E.M.A. method
iv) Load shape
Immediately prior to the point of tangency of the belt and pulley the load shape may be approximated by a segment of a circle whose area is equal to that of the cross-sectional area of the material on the normal trough portion of the conveyor belt. This takes standard edge distances into consideration as well as the material's surcharge angle.v) Separation Angle
The angular direction of the trajectory is determined by the forces acting on the material at its center of mass. The techniques does not include the effects of:
Frictional forces between material and belt.
Inertia effects of the material on the belt
Adhesive properties of the material
2.1.1 Material stream pattern
The resulting plot of the material trajectory yields a parallel path for material flow if the materials "apparent" density is above 800 kg, and roughly is of uniform particle size. If the material free fall more than 2 m, is light and fluffy, or is discharged from a very high speed belt is slightly divergent path will be followed.
2.2 M.H.E.A
The M.H.E.A.'s approach is essentially the same as that of the C.E.M.A. taking a tabulated form for the most common arrangements of :
Belt width
Trough angle
Material surcharge angle
And using these to obtain the distance to the center of mass from the pulley center line.
2.2 Dunlop Conveyor Manual
The Dunlop Conveyor Manual divides the trajectory derivation into two methods.
Fast conveyors which are those that do not fall within the limits of their chart
Slow conveyors
2.3.1 Slow Conveyors
When the belt runs slowly enough for the material to ride around the pulley it is classified as a slow conveyor. When this happens the material starts flowing downhill chasing its own angle of repose. It then extends longitudinally, gaining a speed in excess of that imparted by the belt forcing it to leave the belt earlier and at a speed greater than the belt. This tends to throw the material "further out". The throw of the material as it leaves the belt is a function of:
Belt speed
Pulley diameter
Material flow characteristics.
After it has left the belt the trajectory is influenced by:
Material density and grain size
Wind currents
The Dunlop method for slow conveyors uses a chart to obtain the separation angle and a matching distance measured along the tangent line designated as X in Fig. 2. The chart has been derived by considering the limiting conditions causing slip between the material and belt. The point at which slip takes place is governed by the materials friction characteristics on the belt. The coefficient of friction in the Dunlop chart has been set to an unspecified constant limiting the separation angle a material can have to 62.
This technique does not take into account:
Inertia effects of the material on the belt.
Material adhesion characteristics
Belt thickness
Belt width
Material surcharge angle
Load shape on the belt, or
Edge distances
And leaves the user guessing what to do about the pulleys smaller than 312mm diameter.
2.3.2 Fast Conveyors
A more traditional approach is used here, concentrating only on the belt velocity. The material leaves the belt at the point of tangency with the belt and pulley and travels at belt speed in the tangential direction while falling under the effects of gravity.
2.3.3 Material stream pattern
Dunlop mentions nothing about whether the material stream:
expands along its flight path
remains parallel
contracts
There is, however, an implied form of contraction given in the example drawings and shown in Fig. 2.
Fig 2. Dunlop method
2.4 Booth
Booth analyzed the forces acting on a particle slipping down the curve of the discharge pulley. In this analysis he included the effects of friction between the particle and the belt but did not take into account the particles' inertia or any adhesion they may have with the belt. A static coefficient of friction of the belt of 0.55 is suggested for use with 'hard rock', but values for other materials are not given. As well as an analytical method for determining he separation point and discharge velocity a monogram is presented which covers a wide range of belt speeds and pulley diameters. Booth's method is essentially an analytical approach which parallels the graphical method in the Dunlop Conveyor Manual and the same comments more or less apply to it as those stated in sections 2.3.2 and 2.3.3.
2.3 Korzen
The analysis carried out by Korzen strived to take into account the affects of friction (both static and kinematics) as well as inertial and adhesion of the material on the belt. All of these factors play an important role in determining the separation point and discharge velocity of the material from the belt. To complete the analysis the affects of air drag were included to help describe the trajectory after the material had left the belt.
2.5.1 Slow Conveyors
Slow conveyors are characterized by the material wrapping to some extent around the head pulley before discharging. Wrap will occur if:
(v2b / rg) - (σa / γhb) < cosθ (1)
where:
σa = adhesion [kPa]
γ = specific weight
vb = conveyor belt velocity
hb = material height on belt [m]
r = radius of discharge pulley plus belt [m]
g = acceleration due to gravity
θ = bulk solid stream discharge angle measured from the vertical []Very high adhesive stresses will result in some of the3 material staying in contact with the belt and being carried back while the rest of the burden will reach a stress level where it will fail within itself and fall off the pulley at some stage of the wrap. This method assumes that either all of the material will separate at the calculated critical angle or, if the adhesion is high enough that it will all carry back to be dealt with by the belt cleaners.
2.5.2 Fast Belts
When the material fails to wrap around the head pulley it is taken as having the belt velocity and ejected accordingly, suffering only the affects of air drag after separation. The condition leading to this occurring will be satisfied if:
(v2b / rg) - (σa / γhb) < cosαb (1)
where:
αb = conveyor belt inclination angle []
The trajectory path is plotted in the same way as the Dunlop/Booth method and a converging stream pattern is recommended.
2.5.3 Air drag
Air drag is taken into account by using a multi-step approximation method to solve the relevant expressions developed by Korzen in his paper. To solve these the particle's solid density, equivalent diameter, and correction factors allowing for the effect of grain shape on the air drag coefficient must first be obtained as well as the properties of the atmospheric air. With this information a value for the coefficient of air drag can be obtained which can be used to modify the amount of vertical fall the particle undergoes for any given amount of horizontal excursion. It also is stated that air drag affects are not critical on particles that have amass greater than 1g.
2.6 Hill and Arnold
This method is essentially a compilation of most of the previously discussed techniques. It consists of an interactive "Autolisp" program using C.E.M.A.'s equations to determine the center of mass of the load shape and expanding this to take into account conveyors with only two troughing idlers which are not available in the M.H.E.A. & C.E.M.A. publications.
Options are available to plot the following methods:
C.E.M.A., M.H.E.A
Dunlop, fast and slow
Booth
Korzen, with or without air drag affects.
The output can be used directly in "Auto-CAD" based drawings, and provides a useful too in positioning:
Transfer chutes
Receiving bins
Weighing devices
Rock boxes and
Impact plates
With greater accuracy and speed than previously possible.
3. EXPERIMENTAL PROGRAM
With the accuracy available from CAD system and the choice of so many different trajectory profiles it was decided to conduct experiments to find out which profile more closely matched that obtained from a real conveyor system.
3.1 Large Scale Experimental Test Facility
A large scale experimental test facility was set up to investigate transfer chutes and methods for improving their design.
This system of variable speed conveyors was utilized to test the different material trajectory predictions using washed coal at approximately 10% MWB. This material showed only 0.115 kPa adhesion to the belt a value that displays no readily discernable difference in the shape of the material trajectory between the Korzen and Dunlop/Booth methods at low speeds.
3.2 Test Procedure
To carry out the investigation into material trajectory paths a full scale drawing of the two most likely contenders, C.E.M.A. and Dunlop/Booth was made on a CAD system using the interactive "Autolisp" program, the Korzen method was not tested as the resulting trajectory output matched that of the Dunlop/Booth path due to the low adhesion value if the material and the average particle mass being greater than 1 g. A video camera with high speed shutter capability and a still camera were used to record the path followed by the material. The cameras were set up to view, as squarely as possible, the center of one of the trajectory paths near the end of the material's flight path to avoid any parallax error.
3.2 Results of Experimental Program
The main series of test were carried out at 2 ms-1 and 4 ms-1 though observations were made at slow velocities down to 0.5ms-1. Simulations were carried out using the computer model to examine the effects of materials with high adhesion and varying particle size.
All test runs carried out showed that the Dunlop/Booth method provided a more accurate prediction of the path followed by the bulk solid. This was increasingly evident as the belt velocity increased to 4 ms-1 (Fig. 3) at which point a C.E.M.A. plot would have taken the material over the edge of the receiving bin and onto the floor.
For slow speed conveyors a Dunlop/Booth trajectory provided better correlation than did the C.E.M.A., M.H.E.A. methods which tended to wrap the material too far around the pulley (Fig. 4).
The Dunlop/Booth/Korzen method possesses a greater accuracy for fast belts than the others because it does not assume that the material accelerates to the tangential velocity of the center of mass as does the C.E.M.A.. This difference becomes more noticeable as the load shape becomes larger and sits higher on the belt.
The material stream on the higher speeds tests showed a tendency to remain parallel or slightly converge near the end of its flight.
Fig. 3: Material trajectory comparisons for Dunlop and C.E.M.A. at 4m/s
Fig. 4: Material trajectory comparisons for Dunlop and C.E.M.A. at 0.5m/s
Comparing the Dunlop/Booth method with that of Korzen shows only a slight variation in the separation angle (θ) when using a simple bulk solid or one in which the adhesive stress is low say up to 0.5 kPa.
The material system pattern remains more or less parallel showing only slight spreading. The pattern will widen with cohesive materials and slower belt velocities as the particles tend to get carried back around the pulley further before departing. However, this is not a significant proportion of the main stream.
The bulk of the material on the low speed belt followed a parallel path with some slight spreading becoming noticeable near the end of its flight.
Air drag will have a significant affect on low density fine particles with a typical mass lower than 1 g. This was not observed during the experimental work carried out by running simulations with the computer model using the material properties for the coal in the test rig. It was found that using a test head pulley diameter of 800 mm on a typical troughed belt running at 2 ms-1 the particles of coal had to be under 0.001 m to affect the material stream path by more than a 160 mm of offset after falling through a vertical distance of three meters. Higher belt speeds produce even higher air drag on the particles and this further increases the rate at which the material stream will fall short of its intended mark when air drag is not taken into account.
Material that exhibits high adhesive stress characteristics of the order of 0.3 kPa and above will start to carry back further around the head pulley significantly affecting the final impact area after falls of more than 2 m.
4. CONCLUSIONS
The Dunlop/Booth method for predicting material trajectories provides a more reliable method for determining the flight path of a simple bulk solid than either the C.E.M.A. or M.H.E.A. It is much easier to apply than that of Korzen and less information is needed about the material's properties.
This is particularly important for the placement of any devices in a fast moving material stream such as weighing mechanisms or rock boxes where an error such as that introduced by the C.E.M.A. method could render the device ineffective.
While the differences in trajectory paths becomes less pronounced as the belt velocity decreases, the Dunlop/Booth curve is still the better as depicted in Fig. 4. For simple bulk solid with average particle mass above 1 g.
5. RECOMMENDATIONS
The best material trajectory prediction results from combining both C.E.M.A. and Dunlop/Booth methods together. This results in a plot whose inner curve is determined by the Dunlop/Booth method foe either fast or slow conveyors and the outer curve drawn either parallel to it for fast belts or at the velocity of the center mass to give a slightly diverging material pack for slow belts.
If the material under investigation displays a large amount of adhesion, tests should be carried out to determine the magnitude of the adhesive stress and the value of the friction coefficient between the materials and the belt and Korzens method used.
If the material to be handled is 'free flowing' and its average particle mass is greater than 1 g then it is simpler to utilize the Dunlop/Booth method as less information is needed about the materials properties. Using friction coefficient of about 0.55 will suffice for most materials that might be described by the term 'hard rock' that is, materials that tend to behave close to a simple bulk solid displaying only small amounts of adhesion, say, typically less than 0.3 kPa.
ACKNOWLEDGEMENTS
The authors wish to acknowledge the financial support provided by the National Energy Research Development and Demonstration Council under Project 1.188 ' Blockage Wear and Conveyor Direction Change of Conveyor Chutes.
REFERENCES
1. Recommended Practice for Troughed Belt Conveyors published by The Mechanical Handling Engineers Association 1986.
2. Booth E.P.O.: Trajectories From Conveyors Method calculating Them Corrected, Engineering and Mining Journal Vol. 135 - 1934)
3. Korzen, Z : Mechanics of Belt Conveyor Discharge Process Affected by Air Drag; bulk solids handling Vol. 9 (1989) No. 3
4. Dunlop Conveyor Manual; Dunlop Industrial - 1982
5. Belt Conveyors for Bulk Materials; published by C.E.M.A; CBI Publishing Company, 2nd Edition - 1979.
