Modern Technological Developments in the Storage and Handling of Bulk Solids

A. W. Roberts
Director, School of Engineering, Director TUNRA Ltd,
The University of Newcastle, NSW, Australia

Acknowledgements : Bionic Research Institute - Chute Design Conference 1992

SUMMARY

This paper presents an overview of some modern developments in the technology of bulk solids handling. An overview of storage system design including bins and gravity reclaim stockpiles is presented and aspects of feeder performance is given. The importance of wall or boundary friction in hopper and chute design is discussed and the associated adhesion and wear characteristics are outlined in relation to the selection of appropriate lining materials. Problems due to flow instabilities during discharge from coal bins are reviewed; these flow pulsations may give rise to severe dynamic loads on the bin structure.

1. INTRODUCTION

Throughout the world bulk materials handling operations perform a key function in a great number and variety of industries. While the nature of the handling tasks and scale of operation vary from one industry to another and, on the international scene, from one country to another according to the industrial and economic base, the relative costs of storing, handling and transporting bulk materials are, in the majority of cases, very significant. It is important, therefore, that handling systems be designed and operated with a view to achieving maximum efficiency and reliability .Directly related to these objectives is the ongoing need for engineers and those involved in the operation of handling plants to be kept informed of the latest research and technological developments relevant to their industry and, at the same time, contributing to these developments and to the dissemination of information in the light of their own experiences.

The theme embodied in the foregoing remarks is of particularly relevance to Australia in view of the heavy dependence on bulk handling operations. While these operations range across the broad spectrum of industries, of prime importance are the mining and mineral processing industries which handle coal and mineral ores in large tonnages. These industries make a major contribution to Australia's export earnings and economic growth.

Over the past three decades much progress has been made in the theory and practice of bulk solids handling. Reliable test procedures for determining the strength and flow properties of bulk solids have been developed and analytical methods have been established to aid the design of bulk solids storage and discharge equipment. There has been wide acceptance by industry of these tests and design procedures and, as a result, there are numerous examples throughout Australia of modem industrial bulk solids handling installations which reflect the technological developments that have taken place.

Notwithstanding the current situation, the level of sophistication required by industry demands, in many cases, a better understanding of the behaviour of bulk solids and the associated performance criteria for handling plant design. Experience indicates that the solution one problem which leads to an improvement in plant performance often exposes other problems which need to be solved. It becomes progressively clearer that there are many gaps in the present state of knowledge where further research is necessary.

The purpose of this paper is to briefly highlight the present state of knowledge associated with bulk handling and indicate where further work is necessary. The material presented is based on the research conducted by Tunra Bulk Solids Handling Research Associates of the University of Newcastle. This research group has been involved in bulk handling research and industrial consulting for some considerable time and in recent years has been .supported by research grants obtained from AMIRA.

2. HANDLING PLANT DESIGN - BASIC CONCEPTS

2. 1 General Remarks

The design of handling plant, such as storage bins, gravity reclaim stockpiles, feeders and chutes is basically a four step process:

1. Determination of the strength and flow properties of the bulk solids for the worst likely flow conditions expected to occur in practice.
2. Determination of the bin, stockpile, feeder or chute geometry to give the desired capacity, to provide a flow pattern with acceptable characteristics and to ensure that discharge is reliable and predictable.
3. Estimation of the loading on the bin and hopper walls and on the feeders and chutes under operating conditions.
4. Design and detailing of the handling plant including the structure and equipment.

The general theory pertaining to gravity flow of bulk solids and associated design procedures are fully documented [1-4]. For the purpose of the present discussion, the salient aspects of the general philosophy are briefly reviewed.

2.2 Modes of Flow in Bins of Symmetrical Geometry

As is now well established, there are two basic modes of flow, namely, mass-flow and funnel-flow. These are illustrated in Figure 1.

In mass-flow, the bulk solid is in motion at every point within the bin whenever material is drawn from the outlet. There is flow of bulk solid long the walls of the cylinder (the upper parallel section of the bin) and the hopper (the lower tapered section of the bin). Mass-flow guarantees complete discharge of the bin contents at predictable flow rates. It is as a first-in, first-out flow pattern; when properly designed, a mass-flow bin can re-mix the bulk solid during discharge should the solid become segregated upon filing of the bin. Mass-flow requires steep, smooth hopper surfaces and no abrupt transitions or in-flowing valleys.

Mass-flow bins are classified according to the hopper shape and associated flow pattern. The two main hopper types are conical hoppers which operate with axi-symrnetric flow and wedged-shaped or chisel-shaped hoppers in which plane-flow occurs. In plane-flow bins, the hopper half-angle a will usually be, on average, approximately 8 to 10 larger than the corresponding value for axi-symmetric bins with conical hoppers.

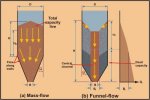
Figure 1. Modes of Flow

Therefore, they offer larger storage capacity for the same head room than the axi-symmetric bin, but this advantage is somewhat offset by the long slotted opening which can give rise to feeding problems. The transition hopper, which has plane-flow sides and conical ends, offers a more acceptable opening slot length. Pyramid shaped hoppers, while simple to manufacture, are undesirable in view of build-up of material that is likely to occur in the sharp corners or in-flowing valleys. This may be overcome by fitting triangular-shaped gusset plates in the valleys.

Funnel-flow occurs when the hopper is not steeply sloped and the walls of the hopper are not smooth enough. In this case, the bulk solid sloughs off the top surface and falls through the vertical flow channel that forms above the opening. Flow is generally erratic and gives rise to segregation problems. Flow will continue until the level of the bulk solid in the bin drops an amount HD equal to the draw-down. At this level, the bulk strength of the contained material is sufficient to sustain a stable rathole of diameter D_f as illustrated in Figure 1(b). Once the level defined by H_D is reached, there is no further flow and the material below this level represents 'dead' storage. This is a major disadvantage of funnel-flow. For complete discharge, the bin opening needs to be at least equal to the critical rathole dimension determined at the bottom of the bin corresponding to the bulk strength at this level. However, for many cohesive bulk solids and for the normal consolidation heads occurring in practice, ratholes measuring several metres are often determined. This makes funnel-flow impracticable. Funnel-flow has the advantage of providing wear protection of the bin walls, since the material flows against stationary material. However it is a 'first-in last-out' flow pattern which is unsatisfactory for bulk solids that degrade with time. It is also unsatisfactory for fine bulk solids of low permeability. Such materials may aerate during discharge through the flow channel and this can give rise to flooding problems or uncontrolled discharge.

The disadvantages of funnel-flow are overcome by the use of expanded-flow, as illustrated in Figure 2. This combines the wall protection of funnel-flow with the reliable discharge of mass-flow. Expanded-flow is ideal where large tonnages of bulk solid are to be stored. For complete discharge, the dimension at the transition of the funnel-flow and mass-flow sections must be at least equal to the critical rathole dimension at that level. Expanded-flow bins are particularly suitable for storing large quantities of bulk solids while maintaining acceptable head heights. The concept of expanded-flow may be used to advantage in the case of bins or bunkers with multiple outlets.

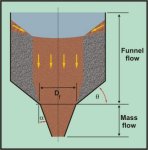
Figure 2. Expanded Flow

Generally speaking, symmetric bin shapes provide the best performance. Asymmetric shapes often lead to segregation problems with free flowing materials of different particle sizes and makes the prediction of wall loads very much more difficult.

2.3 Mass-Flow and Funnel-Flow Limits for Symmetrical Bins

(a) Established Theory due to Jenike

The mass-flow and funnel-flow limits have been defined by Jenike on the assumption that a radial stress field exists in the hopper [1,2]. These limits are well known and have been used extensively and successfully in bin design. The limits for axi-symmetric or conical hoppers and hoppers of plane-symmetry depend on the hopper half-angle α, the effective angle of internal friction 8 and the wall friction angle Φ. Once the wall friction angle and effective angle of internal friction δ have been determined by laboratory tests, the hopper half-angle may be determined. In functional form

α = ( Φ,δ ) ------------------- (1)

The bounds for conical and plane-flow hoppers are plotted for three values of δ in Figure 3. In the case of conical or axi-symmetric hoppers, it is recommended that the half-angle be chosen to be 3 less than the limiting value. For plane-flow, the bounds between mass and funnel-flow are much less critical than for conical hoppers. In plane-flow hoppers, much larger hopper half angles are possible which means that the discharging bulk solid will undergo a significant change in direction as it moves from the cylinder to the hopper.

For plane-flow, the design limit may be selected; if the transition of the hopper and cylinder is sufficiently radiused so that the possibility for material to build-up by adhesion is significantly reduced, then a half-angle 3 to 4 larger than the limit may be chosen.

Figure 3. Limits for Mass-flow for Conical and Plane-Flow Channels

(b) Modification to Mass-Flow Limits - More Recent Research

Since in the work of Jenike, flow in a hopper is based on the radial stress field theory, no account is taken of the influence of the surcharge head due to the cylinder on the flow pattern developed, particularly in the region of the transition. It is been known for some time that complete mass-flow in a hopper is influenced by the cylinder surcharge head. For instance, there is a minimum level Hcr which is required to enforce mass-flow in the hopper [5]. For the mass-flow bin of Figure 1(a), this height ranges from approximately O.75D to 1.0 D.

More recent research has shown that the mass-flow and funnel-flow limits require further explanation and refinement. For instance, Jenike [6] published a new theory to improve the prediction of funnel-flow; this led to new limits for funnel-flow which give rise to larger values of the hopper half-angle than previously predicted, particularly for high values of the wall friction angle. In the earlier theory, the boundary between mass-flow and funnel-flow was based on the condition that the stresses along the centre line of the hopper became zero. In the revised theory the flow boundary is based on the condition that the velocity becomes zero at the wall.

In a comprehensive study of flow in silos, Benink [7] has identified three flow regimes, mass-flow, funnel-flow and an intermediate flow as illustrated in Figure 4. Whereas the radial stress theory ignores the surcharge head, Benink has shown that the surcharge head has a significant influence on the flow pattern generated. He derived a fundamental relationship for Hcr in terms of the various bulk solid and hopper geometrical parameters, notably the H/D ratio of the cylinder and the effective angle of internal friction δ. Benink developed a new theory, namely the arc theory, to quantify the boundaries for the three flow regimes. This theory predicts the critical height Hcr at which the flow changes.

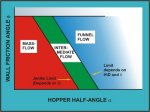
Figure 4. Flow Regimes for Plane-Flow Hopper defined by Benink [7]

2.4 Bin Geometry for Mass-Flow

(a) Basic Considerations

Basically the aim in mass-flow design is to determine the hopper geometry to give reliable flow at all times at the required discharge rate. Primarily, the requirement is to determine the hopper half angle α, which defines the slope with respect to the vertical, and opening dimension B.

Undisturbed storage time and changes in moisture content can significantly influence the unconfined yield strength of the bulk solids. By way of illustration, the critical hopper opening dimension B for three Hunter Valley coals plotted as a function of moisture content are shown in Figure 5. This figure shows three coal samples, Sample (1) being a Raw Open Cut Coal, Sample (2) a washed version of (1) and Sample (3), a blend of (2). The high strength of the raw, unwashed coal is clearly evident. Experience has shown that the peak bulk strength of coal may occur at a moisture content somewhere between 70% and 90% of the saturation limit.

(b) Influence of Wall Friction

Since an increase in both the normal wall pressure and consolidation pressure accompany an increase in hopper span, then the corresponding decrease in wall friction angle will permit the hopper half angles to be increased. Hence it is possible to calculate a hopper half angle α as a function of hopper span or opening dimension as indicated in Figure 6. As shown, the half hopper angles for both wedge and conical hoppers tend towards limiting values as the opening dimension increases.

2.5 FUNNEL-FLOW AND EXPANDED-FLOW GEOMETRY

As previously discussed, it is necessary to compute the critical or minimum diameter Df for an unstable pipe or "rat-hole" from which the minimum bin opening for funnel-flow or the transition dimension for expanded-flow is determined. The transition dimension for expanded-flow refers to the transition of the mass-flow hopper with the upper funnel-flow section of the bin.

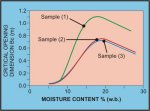
Figure 5 Critical Opening Dimension BCR as a Function of Moisture Content for Three Coal Samples -Stainless Stee1304-2B Lining

Figure 6 Variation of Hopper Half-Angle with Span for Coal on 304-2B Stainless Steel

3. BIN WALL LOADS

In bin design, the prediction of bin wall loads continues to be a subject of some considerable complexity. In view of its obvious importance it is a subject that has, in recent years, attracted a good deal of research effort. Currently, there are several research groups in various countries of the world directing their attention to the study of bin wall loads using a range of analytical and numerical techniques such as those involving finite element analysis. Despite the widely varying approaches to the analysis of bin wall loads, it is clear that the loads are directly related to the flow pattern developed in the bin.

The flow pattern which a mass-flow bin exhibits is reasonably easy to predict and is reproducible. However, in funnel-flow bins the flow pattern is more difficult to ascertain, especially if the bin has multiple outlet points, the loading of the bin is not central and/or the bulk solid is prone to segregation. Unless there are compelling reasons to do otherwise, bin shapes should be kept simple and symmetric.

3.1 Wall Pressures in Mass-Flow Bins

In mass- flow bins, the pressures acting normal to bin walls vary from the static or filling conditions to the dynamic or flow conditions. The pressure distributions are well defined and, using current theories [3-4], may be predicted with confidence.

It is to be noted that in the flow situation a high switch stress occurs at the transition. The magnitude of this switch stress is several times the corresponding static value. Further, it may also be noted that the wall pressures acting in the cylindrical section during flow may be higher than the static values. For a perfectly parallel cylinder, the wall pressures during flow would be the same as the static values. However, when imperfections such as weld projections or plate shrinkage give rise to flow convergences, peak stresses occur. The stresses are taken into account by computing the locus of all such possible peak pressures.

3.2 Wall Pressures in Funnel Flow Bins

While for design purposes wall pressures in symmetrical funnel-flow bins may be determined with a high degree of confidence, the wall loading in bins with multiple outlets and eccentric discharge points are far more difficult to estimate. Under eccentric discharge, the walls are subject to bending moments and hence, bending stresses in addition to hoop stresses [8]. In the case of tall grain silos, the use of anti-dynamic tubes offers significant advantages in controlling the wall pressures, both in the case of symmetrical funnel-flow silos as well as silos with eccentric load out points [9-10].

3.3 Australian Standard for Loads in Bulk Solid Containers

In recent years there has been considerable activity in several countries of the world in the development of new or revised codes for bin wall loads. Of particular note is the preparation of the new Australian Standard "AS-89138 Loads for Bulk Solids Containers " [11], which represents a major milestone. This publication presents a very comprehensive review of the loads acting in bin and silo walls under a the full range of operating conditions likely to occur in practice. As an example, Figure 7 shows the wall loadings determined on the basis of this new Standard for a large coal bin having seven outlets; the pressure profiles correspond to one possible mode of discharge involving the operation one eccentric outlet only.

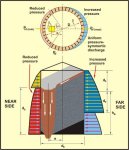
Figure 7. Circumferential Pressure Variation due to Operation of One Eccentric Outlet

4. FEEDING OF BULK SOLIDS

4.1 Use of Feeders to Control Discharge

In general, a feeder is a device used to control the flow of bulk solids from a bin. While there are several types of feeders commonly used, it is essential that they be selected to suit the particular bulk solid and the range of feed rates required. It is particularly important that the hopper and feeder be designed as an integral unit so as to ensure that the flow from the hopper is fully developed with uniform draw of material from the entire hopper outlet. For example, in the case of a screw feeder, this is achieved by using selected combinations of variable pitch, variable diameter and variable core or shaft diameter.

In the case of a belt or apron feeder, a tapered opening is required as illustrated in Figure 8. The use of vertical triangular plates in the hopper bottom are an effective way to achieve the required taper. The gate on the front of the feeder is used only for flow trimming and not for controlling the flow rate. The height of the gate is adjusted to give the required release angle Ψ to achieve uniform draw along the slot. Once correctly adjusted, the gate is then fixed in position and the feed rate is controlled by varying the speed of the feeder.

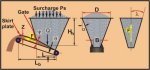
Figure 8. Belt and Apron Feeder

In the case of vibratory feeders, there is a tendency for feed to occur preferentially from the front. To overcome this problem, it is recommended that the slope angle of the front face of the hopper be increased by 5 to 8 as illustrated in Figure 9. Alternatively, the lining surface of the front face in the region of the outlet may selected so as to have a higher friction angle than the other faces.

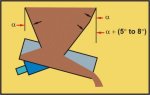
Figure 9. Vibratory Feeder

4.2 Determination of Feeder Loads and Power

The determination of feeder loads and drive powers requires a knowledge of the stress fields generated in the hopper during the initial filling condition and during discharge. Under filling conditions, a peaked stress field is generated throughout the entire bin as illustrated in Figure 10. Once flow is initiated, an arched stress field is generated in the hopper and a much greater proportion of the bin load is supported by the hopper walls. Consequently, the load acting on the feeder substantially reduces as shown in Figure 10.

Figure 10. Load Variations on a Feeder

It is quite common for the load acting on the feeder under flow conditions to be in the order of 20% of the initial load. The arched stress field is quite stable and is maintained even if the flow is stopped. This means that once flow is initiated and then the feeder is stopped while the bin is still full, the arched stress field is retained and the load on the feeder remains at the reduced value. The subject of feeder loads is discussed in some detail in Refs. [12-15]. The loads on feeders and the torque during start-up may be controlled by ensuring that an arched stress field fully or partially exists in the hopper just I prior to starting. This may be achieved by such procedures as:

Cushioning in the hopper, that is leaving a quantity of material in the hopper as buffer storage.

Starting the feeder under the empty hopper before filling commences.

Raising the feeder up against the hopper bottom during filling and then lowering the feeder to the operating condition prior to starting. In this way an arched stress field may be partially established.

5. GRAVITY RECLAIM STOCKPILES

5.1 Draw-Down Performance Considerations

Gravity reclaim stockpiles when properly designed, operate under expanded-flow, as illustrated in Figure 11. This shows discharge through a single opening in a stockpile. Discharge will take place by funnel-flow in the main body of the stockpile, with the flow expanded through the mass-flow hopper. In this way, reliable flow to the feeder is assured. Flow will continue until the draw-down head hD is reached; flow then ceases as a stable pipe or rathole is formed. The draw-down is consistent with critical rathole dimension Df which forms at that level. The shape of the rathole depends on the consolidation conditions within the stockpile, the particle or lump size range of the stored bulk solid and the moisture content.

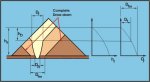
Figure 11. Draw-Down in Stockpile

Complete draw-down, as illustrated in Figure 11, corresponds to the critical rathole dimension Dfm at the base of the stockpile. For complete draw-down to occur, it is necessary for the diagonal dimension of the hopper transition to be at least equal to Dfm Since values of Dfm may be several metres, often it is not practical or economical to employ a large enough hopper to achieve complete draw-down. For this reason, the design of stockpile reclaim hopper and feeder systems requires a full consideration of the various options available with a view to optimizing the reclaim performance within specified practical and economic limits.

5.2 Use of Multiple Hoppers

The use of multiple hopper systems which allows for intersection of the flow channels to occur, as illustrated in Figure 12, provides for good reclaim performance to be achieved. By varying the separation distance X, an optimum spacing can be established as illustrated in Figure 13.

5.3 Live Capacity versus Moisture Content

In a programme of research conducted at the University of Newcastle 16,17], studies have been performed using a conical stockpile model which allowed different feeder configurations to be examined. Although the scale of the model relative to actual stockpiles is very small (a factor of 1/50 in one case of an iron ore stockpile), the predicted performance base on the model studies were surprisingly good. The modelling process involves scaling the particle size and adjusting the moisture content of the bulk solid to reproduce, as close as possible, the same arching characteristics in the model feed hoppers as would occur in the full scale stockpile.

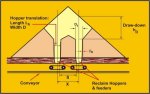
Figure 12. Improved Reclaim Performance using Double Reclaim System

Figure 13. Live Capacity versus Feeder Separation

By way of illustration, Figure 14 shows the reclaim performance for a double hopper system for five different coal moisture contents. Several tests were conducted over a range of hopper separation lengths. The separation of the hopper is measured by the distance S between the inner edges of the two hoppers which are equi-distant on each side of the stockpile centreline.

The data in Figure 14 show the reduction in live capacity with increase in moisture. This is to be expected because the strength of the bulk solid increases with moisture content. The results also show that there is an optimal separation length for the two-hopper system where maximum reclaim of material can be expected. This optimal distance being dependent on the moisture content of the bulk material.

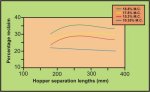
Figure 14. Double Hopper Stockpile Live Capacity for Model Stockpile using Coal. Hopper length at transition = 12Omm, width = 100mm

5.4 Loads on Reclaim Hoppers and Feeders

The loads on reclaim hoppers and feeders and the corresponding power to drive the feeders varies from the "initial" to the flow condition as discussed in Section 4. The loads are illustrated in Figure 15. The initial load will correspond to the case when the stockpile or crater above the feeder is filled. The surcharge load Qs will depend on the consolidation condition of the bulk solid in the stockpile. The worst case corresponds to the hydrostatic pressure. However, if a rathole has been pre-formed, then the surcharge load will be reduced. When an arched or flow stressed field has been formed within the mass-flow reclaim hopper, the load on the feeder will be greatly reduced. Confirmation of the load conditions acting on reclaim hoppers has been obtained from the model stockpile tests.

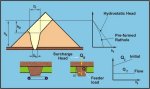
Figure 15. Loads on Stockpile Feeders

6. SURFACE OR WALL FRICTION

6. 1 Selection of Lining Materials

Of the various parameters affecting the performance of hoppers, feeders and chutes, the friction at the boundary surface has, in most cases, the major influence. Judicious choice of lining material to achieve low friction and wear is an important consideration.

There are a great many lining materials and surface coatings on the market, some common linings being illustrated in Table III. Also shown are the bulk materials for which the lining material is commonly used.

While cost is a significant consideration, it is most important that the lining material be selected on the basis of service life and performance. Factors to be considered include:

• Surface friction and adhesion  
• Resistance to impact, if appropriate  
• Method of attachment  
• Installation cost and maintenance
• Resistance to abrasive wear
• Resistance to corrosion
• Initial cost

It is recommended that appropriate tests be conducted to determine the relevant flow properties of the bulk solid and the proposed lining surface. In view of the importance of surface or wall friction, some salient aspects are now reviewed.

6.2 Surface Friction and Adhesion

The adhesion of bulk solid particles to hoppers and chutes is a result of the interaction between the bulk solid and the boundary or wall surface[18-21]. While adhesion and/or cohesion are difficult to measure directly, an indication of these parameters may be gleaned from bulk solid and wall surface friction measurements using a direct shear test apparatus. The parameters of interest are defined in Figure 16. 1.

Figure 16. Wall or Surface Yield Locus (WYL)

The surface friction characteristics are displayed by the wall yield locus W .Y .L.; the surface friction angle Φ is defined as follows: 

Φ = tan^-1 (ﺡ / σ_w) ---------------- (2)

where ﺡ = shear stress at the wall

σw = corresponding normal stress at the surface.

As indicated by Figure 16, the friction angle Φ between the bulk solid and boundary surface decreases as the normal pressure increases. This effect is illustrated in Figure 17.

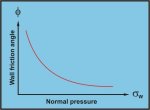
Figure 17. Characteristic Surface or Wall Friction Variation with Normal Pressure

6.3 Interaction Characteristics

Bulk solid/boundary surface friction and adhesion depend on the interaction between three groups of variables, those relating to the bulk solid, those relating to the wall or boundary surface and those which arise from loading and environmental conditions. This interaction is shown, diagrammatically in Figure 18.

Figure 18. Bulk Solid/Boundary Surface Friction Interactions

The relevant properties in each of the three groups are summarised as follows :

(i) Bulk Solid Characteristics -

• Particle size and size distribution

• Panicle shape, hardness and density

• Moisture content

• Bulk density

• Chemical composition

(ii) Wall Surface Characteristics -

• Surface roughness

• Hardness

• Chemical composition

(iii) Loading and Environmental Factors -

• Pressure between bulk solid and wall surface

• Relative rubbing or sliding velocity

• Temperature and humidity or moisture conditions

• Wall vibrations

• Undisturbed contact time

6.4 Wall Friction versus Normal Pressure Characteristics

As an illustration of some of the factors influencing wall or surface friction, a set of wall yield loci graphs are shown in Figure 19 [20]. The bulk solid in this case is coal. Figure 19(a) shows the variation of wall friction for black coal at 10% moisture content on three surfaces, namely, stainless steel type 304 with 2B finish, mild steel polished and mild steel rusted all at the instantaneous or zero storage time condition. In the case of the 120 polished mild steel surface the wall friction was also determined after 72 hours undisturbed contact or storage time is also shown; the high friction in this case is quite considerable with corrosion and adhesion or bonding of coal particles to the steel surface.

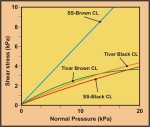
Figure 19(b) compares the Wall Yield Loci for black coal at 19.7% moisture content and brown coal at 65% moisture content on two surfaces, stainless steel type 304 with 2B finish and Tivar 88, an ultra high molecular weight polyethylene material. While in absolute terms the moisture contents of the two coals are significantly different, in relative terms, taking account of their composition and saturated moisture conditions, they are comparable. For the black coal the wall friction angle for stainless steel and Tivar are similar, both exhibiting low friction. This is also the case for brown coal on the Tivar surface. However, the brown coal has abnormally high friction on the stainless steel, despite the smoothness of the surface; the stainless steel is entirely unsuitable for brown coal.

(a) Wall Yield Loci for Black Coal

(b) Wall Yield Loci for Black and Coals

Figure 19. Typical Wall Yield Loci

6.5 Surface Roughness

(a) Roughness Parameters and Effect on Wall Friction

Surface roughness is an important factor in terms of its influence on wall friction. Yet the specification of surface roughness in terms of appropriate parameters which adequately describe the surface is a complex matter requiring careful and detailed consideration.

It is common to simplify surface characteristics in terms of height parameters, such as the centre line arithmetic average roughness (CLA or Ra Number) or RMS roughness. Such parameters are useful for comparison purposes but do not adequately provide an assessment of the interaction between panicle size and surface profile. For this reason, Ooms and Robens [18] have found it useful to specify the surface characteristics in terms of Surface Spectoral Density. This displays the RMS roughness amplitude as a function of frequency where the frequency is the inverse of the roughness wave length.

(b) Roughness Classification of Surfaces used in Bulk Solids Handling

The new Australian Standard on Loads in Bulk Solids Containers [11] designates four surface roughness characteristics Dl to D4. In order that these surface classifications may be quantified in some way, Ooms (Ref. [21]) proposed that the four categories of surfaces be grouped in terms of roughness bands based on the Mean Centreline Roughness or Ra number. Surfaces commonly used have been classified according to this procedure and presented in Figure 20.

Figure 20. Ooms Chan for Lining Surface Roughness Classification

From the discussion in the previous Section, it is apparent that the proposed form of classification is somewhat restrictive in terms of the limited information conveyed by the Ra number. Also the wall roughness may not necessarily remain constant and should be considered as a variable. For instance, a polished or lightly rusted carbon steel surface may become deeply pitted and change from group D2 to group D3. An aluminium surface is easily scored and may change from group Dl to group D2. On the other hand, some stainless steel surfaces will polish during service and may change from group D2 to D 1.

6.5 Influence of Vibrations

Roberts et al [22-24], have shown that the application of vibrations to a wall surface can significantly reduce wall friction and therefore promote flow. Vibrations can also reduce bulk strength, further assisting in promoting gravity flow. The evidence indicates that the best results are achieved by using frequencies of 100 Hertz or higher, and low amplitude.

7. ADHESION OF BULK SOLIDS ON WALLS OR SURFACES

7. 1 Adhesion of Bulk Solids in Chutes

The characteristics of surface or wall friction discussed in the previous section indicate that, for most bulk solids and lining materials, the Wall Yield Loci (WYL) tend to be convex upward in shape. Furthermore the WYL often intersect the shear stress axis corresponding to zero normal pressure indicating an adhesion/cohesion effect as depicted in Figure 18.

Problems due to high wall friction, cohesion and adhesion, which are associated with low pressure conditions, often occur in chutes and standpipes. Cohesion and adhesion can cause serious flow blockage problems when corrosive bonding occurs, such as when moist coal is in contact with carbon steel surfaces. The bonding action can occur after relatively short contact times. Impurities such as clay in coal can also seriously aggravate the behaviour due to adhesion and cohesion.

Transfer chutes should be designed to ensure that satisfactory flow is obtained without flow blockages. Yet despite their apparent simplicity, the flow patterns developed in chutes often not fully appreciated. Occasions have arisen in practice where costly flow interruptions have occurred due to incorrect chute design arising from a lack of understanding of the bulk solid and chute surface friction characteristics.

The design of transfer chutes is discussed in References [25-28]. Consideration should be given to the flow properties of the bulk solid and the characteristics of the chute lining material. Moist coal can adhere to vertical, as well as inclined faces of steel chutes eventually causing blockages. This has been found to occur in practice after only a few hours of operation. Problems of this type have occurred, for example, in conveyor feed chutes in coal screening operations as illustrated in Figure 21. The momentum of the coal particles falling from the screen is usually not sufficient to cause scouring of the chute surfaces and, as a result, build-up and complete blockages have been known to occur.

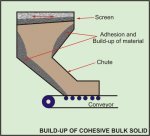
Figure 21. Build-Up of Cohesive Bulk Solid such as Coal on Screen House Conveyor Feed Chute

When determining chute slope angles, account must be taken of the variation of friction angle with change in consolidation pressure, or more particularly, with change in bed depth. Figure 22 shows, for a typical coal, the variation of wall friction angle with bed depth. As indicated, high friction angles can occur at low bed depths, the decrease in friction angle being significant as the bed depth increases.

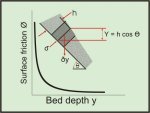
Figure 22 Wall friction angle versus bed depth for bulk solid on chute

The slope θ of the chute should be at least 5 larger than angle of equivalent friction [4].

That is :

 θ_min = tan^-1 [tanΦ (1 + K_v H_o / B)] + 5^o

where Φ = Wall friction angle corresponding to HO

H_o = Bed depth

B = Chute width

K_v = Ratio lateral to normal pressure

K_v will depend on bulk solid properties Normally K_v = 0.5 to 1.0. In the absence of information K_v may be taken to be 0.8.

Often moist bulk solids will adhere initially to a chute surface, but as the bed depth increases, the corresponding decrease in friction angle will cause flow to be initiated. In some cases flow commences with a block-like motion of the bulk solid as depicted in Figure 23.

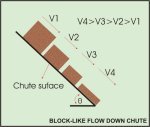
Figure 23 Block-like Flow Down Chute

7.2 Adhesion in Vertical Chutes or Standpipes

Bulk solids, such as coal with high clay contents and at high moisture contents, may adhere to walls of vertical pipes or chutes leading to progressive build-up and flow choking. Problems of this type have been known to occur in the coal handling plant of power stations, as depicted schematically in Figure 24.

Figure 24 Schematic Arrangement of Coal Handling Plant of Typical Power Station

When blockages occur in feed-pipes to the feeder and mill, a boiler may "flame out" in the space of a few minutes. Blockages are initiated by the coal adhering to the pipe wall and then growing inwardly, this action often occurring after only a few tonnes of coal have passed through the system. Often such problems occur when unwashed coal is stored in open stockpiles prior to use. The weathering process can cause the clays to be dispersed, rendering them more likely to adhere to chute and pipe walls. The adhesion process may be aggravated in this case due to the temperature of the mill and standpipe above the mill.

It is important that the pipe or chute diameter be sufficiently large to cause the bulk solid to fall away from the walls. A proposed simplified methodology is presented. Referring to Figure 25, assuming the weight of bulk solid is just sufficient to cause slip along the wall, the required pipe or chute diameter D is given by

D ≥  4ţ  /  ŷ (1 - C² )                                 ------------------ (4)

where :

C = d / D such that C ≥ 0.8

 ţ = shear stress at wall corresponding to normal pressure σ

 ŷ = ρ g = bulk specific weight.

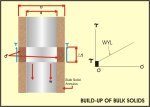
Figure 25 Build-Up of Bulk Solid in Vertical Chute or Standpipe

It is also wise to check whether the pipe diameter is sufficient to prevent a cohesive arch forming. For this analysis, the methods presented in Refs. [3,4] may be used.

8. WEAR IN BULK HANDLING PLANT

Wear in bulk handling plant may result from impact or abrasion or, as is often the case, a combination of both. In addition, deterioration of metal surfaces can occur as a result of corrosion.

8.1 Impact

Erosive type wear due to impact consists of a combination of plastic deformation and cutting wear. Such wear, for example, occurs in pipe bends of pneumatic conveying systems where impact velocities are normally relatively high and where several impacts and rebounds may take place. Normally the particle size is small in this case.

Impact wear also occurs at discharge points of belt conveyors and at entry points to transfer chutes. Velocities of impact are normally relatively low whereas particle size range can be quite wide with large lumps being present.

Impact wear depends on several factors, the relative hardness of the particles and the surface having a significant influence. For impact on hard, brittle materials, the greatest amount of damage occurs when particles impringe at angles of approximately 90. On the other hand, for ductile materials, the greatest amount of erosive wear occurs when particles strike the surface at low angles of attack, usually in the range 15 to 30. Erosive wear due to impact is normally composed of two types, deformation wear and cutting wear.

8.2 Abrasive or Rubbing Wear

This occurs in storage bins and silos particularly in hoppers under mass-flow conditions. Under mass-flow the pressures in a hopper will vary significantly over the hopper surface, with the maximum pressure occurring at the transition, the pressure decreasing towards the outlet. The velocity of the bulk solid adjacent to the wall increases non-linearly from the transition to the hopper outlet. While the magnitude of the velocity at particular point on the hopper wall depends on the bin discharge rate, normally the bulk solid velocities are quite low with pure sliding taking place.

Abrasive wear also occurs in transfer chutes, the flow being characterised by lower pressures and higher velocities than those occurring in hoppers. There are several other areas where abrasive wear is experienced such as in feeders, belt conveyors, vibratory conveyors and screw conveyors. Any mechanical device which involves the motion of bulk solids relative to surfaces will experience wear problems.

8.3 Abrasive Wear Parameters

The concepts of a non-dimensional Relative Wear Number NWR has been introduced [20] in order to permit comparisons to be made between different bin and chute geometries, is defined as :

N_WR = [(σ_w / ŷB) (V_s / V_o) tan Φ

Where :

σ_w = Normal pressure at boundary

ŷ = Bulk specific weight

B = Characteristic dimension, B = outlet dimension in case of hopper; B = chute width in case of chute

V_s = Velocity of sliding at wall

V_o = Sliding velocity at reference location.

For hopper, V_o is defined at transition of cylinder and hopper

For chute, V_o is normally defined at point of entry to chute

Φ = Wall friction angle

8.4 Wear in Mass-Flow Bins

The application of the foregoing to the assessment of relative wear in mass-flow bins has been discussed in Ref. [20]. By way of illustration, the relative wear profiles for axi-symmetric (or conical) and plane-flow bins having the same opening dimension and hopper half angle respectively are illustrated in Figure 26. In the case of the axi-symmetric bins, the maximum relative wear occurs at the outlet, while for the plane-flow bins the maximum relative wear occurs at the transition. In the latter case the wear at the transition is likely to be less than as indicated in Figure 26 owing to the possible build-up of material at the transition. Also, the normal wall pressure occurring at the transition is difficult to predict precisely and is likely to be lower than as indicated.

Some bins are constructed with a variable hopper slope and with the hopper section having different surface textures. Such a bin is discussed in Ref. [29]. The bin in question is axi-symmetric with a capacity of 2400 tonnes. The hopper was lined with 3 mm type 304-2B stainless steel. Examination of the lining after approximately 5 million tonnes of coal had passed through the bin showed that the maximum wear of the stainless steel was around 1mm.

Figure 26 Relative wear profiles for axi-symmetric and plane-flow mass-flow bins 
B = 1.0 m, α = 22, Ф (cylinder) = 30, Ф (hopper) = 20

8.5 Avoidance of Wear Problems due to Eccentric Funnel-Flow

Serious wear problems will occur during funnel-flow where the flow channel or pipe is not fully contained in the bulk solid itself but may incorporate part of the hopper or bin wall. Problems of this nature may occur when bins with eccentric discharge are used, particularly when the bin opening is located near aside wall. On other occasions a badly designed feeder may cause material to pipe adjacent to the hopper wall. Flow channels of this nature give rise to high velocity flow against the wall resulting in accelerated wear.

Often side delivery chutes are incorporated in bins for the purpose of off-loading bulk materials. Side delivery chutes create undesirable flow patterns in bins, leading to accelerated wear of the bin wall in the region of the chute intake as well as in the plates above the chute. This wear is caused by both abrasion and impact Abrasive wear results from the high velocity of the materials during chute discharge, the flow velocity of the materials during chute discharge, the flow following a funnel-flow pattern, as Indicated in Figure 27. The eccentric discharge induces a non-uniform pressure distribution, as shown; bending is induced and the bin shell is deformed as indicated by the dotted curve.

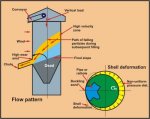
Figure 27 Eccentric discharge due to use of side delivery chutes

Impact wear can occur on filling the bin after discharging from the side delivery chute. The surface is left in a rilled condition as indicated in Figure 27. When filling commences, lumps of bulk material may bounce off the rilled surface and impact the wall in the weakened area above the chute.

It should be noted that despite the fact that side delivery chutes may only be used intermittently, the wear rate during operation is considerable. It is therefore most desirable that side delivery chutes be avoided and incorporate any off-loading via a transfer conveyor operating from the main bin discharge. If side delivery chutes are used, such as an existing installation, it is essential that the bins be lined with wear plates in the region of the chute intakes as well as above the chutes.

8.6 Wear in Transfer Chutes

Abrasive wear in transfer chutes has been discussed in Ref. [18-21]. In the case of straight inclined chutes of constant cross-sectional geometry, the wear is constant along the chute. For chutes of constant curvature, it has been shown that the wear varies along the chute as depicted in Figure 28 reaching a maximum at a particular chute angle and then decreasing. However, the wear is virtually independent of chute radius.

Figure 28. Wear factor for circular curve chutes [20] 
Q = 30 tonnes/hr, V_o = 0.2 m/s, ρ= 1000 kg/m3, b = 0.5 m, E = 0.6, Ф = 30.

8.8 Abrasive Wear Tests

In order to evaluate lining materials for wear resistance, a linear wear tester, as proposed by Roberts [30,31], has been developed jointly at The University of Twente, The Netherlands, and The University of Newcastle, Australia. The tester, which is shown in Figure 29, incorporates the following features:

1. Provision for a continuous supply of "fresh" bulk solid.
2. Provision for the bulk solid normal pressure on the test surface to be varied over the specific range.
3. Provision for the sliding or rubbing velocity to be varied over the specific range.

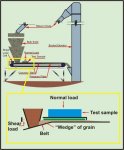
Figure 29. Abrasive Wear Tester

During tests, the friction coefficient, surface roughness, weight and thickness loss are progressively monitored. The teat samples used in the linear wear tests are of similar size to those used in the Jenike Direct Shear Test. This allows cross checking of the wall or boundary friction at various stages throughout the tests. A typical set of test results are illustrated in figure 30.

Figure 30. Comparative Wear Rates for Three Common Lining Materials

9. PULSATING LOADS IN BINS -'SILO QUAKING'

9.1 General Discussion

As is often the case, the solution of one problem which leads to an improvement in plant performance exposes other problems which require further research and development, This applies particularly to gravity flow in storage bins and silos where the application of known theories for reliable discharge, such as by mass-flow, can give rise to dynamic or pulsating flow effects. These effects are normally imperceptible as far as bin discharge is concerned having no detrimental effect on the plant operation. However, the pulsating flow can have a significant influence on the loads acting on bin walls by imposing severe dynamic loads. The phenomenon is often described as 'silo quaking'; it may be linked with the critical head Hcr for mass-flow as discussed in Section 2.

The discussion that follows provides a qualitative view of the 'silo quaking' problem as it r relates to mass-flow, funnel-flow and expanded-flow bins.

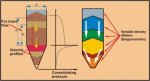
(a) Velocity Profiles and Pressure Distribution (b) Variable Density and Dilation 

Figure 31 Mass-Flow Bin

Referring to the mass-flow bin depicted in Figure 31; as the material flows, it dilates leading to variations in density from the static condition. This is depicted pictorially in Figure 31(b). With H > H_cr, the flow in the cylinder is uniform or 'plug-like' over the cross-section, with flow along the walls. In the region of the transition, the flow starts to converge due to the influence of the hopper and the velocity profile is no longer uniform. The velocity profile is further developed in the hopper as shown. As the flow pressures generate in the hopper the further dilation of the bulk solid occurs. As a result of the dilation, it is possible that the vertical supporting pressures decrease slightly reducing the support given to the plug of bulk solid in the cylinder. This causes the plug to drop momentarily giving rise to a load pulse. The cycle is then repeated.

Studies of the phenomenon of pulsating loads in bins and silos are presently in progress at the University of Newcastle, Australia. In this work, a pilot scale mass-flow, steel silo 1.2m diameter by 3.5 m high and fitted with a stainless steel hopper is being used. The silo is fitted with 14 load cells designed by Prof. V. Askegaard of the Technical University of Denmark; these cells are capable of measuring both normal pressure and wall shear stress. An example of a wall pressure and shear stress records depicting the pulsating load in the cylinder are shown in Figure 32.

Figure 32. Load Cell Records depicting Pulsating Loads in Mass-Flow Bin

A similar action to that described above for mass-flow bins may occur in tall funnel-flow bins or silos where the effective transition intersects the wall in the lower region of the silo. As a result, there is flow along the walls of a substantial mass of bulk solid above the effective transition.

During funnel-flow in bins of squat proportions, where there is no flow along the walls, as depicted in Figure 33, dilation of the bulk solid occurs as it expands in the flow channel. As a result some reduction in the radial support given to the stationary material may occur. If the hopper is fairly steeply sloped, say [θ ≥ δ], then the stationary mass may slip momentarily causing the pressure in the flow channel to increase as a result of the 'squeezing' action. The cycle then repeats.

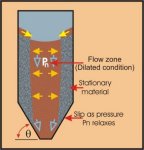
Figure 33 Funnel Flow Bin

A similar behaviour may occur in expanded flow bins, such as the bin depicted in Figure 2 .Pulsating loads can occur in such bins, particularly if the slope angle e of the transition is too steep. Owing to segregation on filling, larger size particles are more likely to be located adjacent to the sloping surface at the lower end of the funnel-flow section. Such particles tend to roll as well as slide, aggravating the load slipping problem and giving rise to load pulsations. Problems of this type have been experienced in large coal bins.

7.2 Multi-Outlet Coal Bins

Silo-quaking problems have been known to occur in bins with multiple outlets. By way of illustration, consider the large coal bin shown in Figure 34. The bin has seven outlets, six around an outer pitch circle and one located centrally. The hopper geometries provide for reliable flow permitting complete discharge of the bin contents. Coal was discharged by means of seven vibratory feeders onto a centrally located conveyor belt. When the bin was full or near full, severe shock loads were observed at approximately 3 second intervals during discharge. The discharge rate from each feeder was in the order of 300 t/h. When the level in the bin had dropped to approximately half the height, the shock loads had diminished significantly. With all the outlets operating, the effective transition was well

Figure 34 Multi-Outlet Coal Bin

down towards the bottom of the bin walls and the critical head H_m was of the same order as the bin diameter and greater than D_F. Substantial flow occurred along the walls, and since the reclaim hoppers were at a critical slope for mass and funnel-flow as determined by flow property tests, the conditions were right for severe 'silo quaking' to occur.

Confirmation of the mechanism of silo quaking was obtained in field trials conducted on the bin. In one series of tests the three feeders along the centre line parallel with the reclaim conveyor were operated, while the four outer feeders were not operated. This induced funnel-flow in a wedged-shaped pattern as indicated in Figure 34, with the effective transition occurring well up the bin walls, that is H_m < H_cr (= D_F ) or H_m << D. The same was true when only the central feeder (Fdr. 1) was operated; in this case the stationary material in the bin formed a conical shape. Under these conditions, the motion down the walls was greatly restricted and, as a result, the load pulsations were barely perceptible.

In a second set of trials, the three central feeders were left stationary, while the four outer feeders were operated. This gave rise to the triangular prism shaped dead region in the central region, with substantial mass-flow along the walls. The load pulsations were just as severe in this case as was the case with all feeders operating. Dynamic strain measurements were made using strain gauges mounted on selected support columns. When the bin was full (or near full), the measured dynamic strains with Hm Hcr were in the order of 4 times the strains measured when the flow pattern was controlled so that Hm < Hcr.

10. CONCLUDING REMARKS

In this paper an overview of some salient aspects of the storage, flow and handling of bulk solids has been presented. It is quite clear that, in recent years, significant advances have been made in research and development associated with bulk handling systems. It is gratifying to acknowledge the increasing industrial awareness and acceptance throughout the world and particularly in Australia of modern bulk materials handling testing and plant design procedures. These procedures are now well proven, and while much of the industrial development has, and still is, centred around remedial action to correct unsatisfactory design features of existing systems, it is heartening that in many new industrial operations the appropriate design analysis and assessment is being performed prior to plant construction and installation. It is most important that this trend continues.

The paper has indicated, by way of example, the ongoing need for research and development which is necessary as industrial plant and processes become more sophisticated, the demands for better quality control become more stringent and both national and international competition requires more efficient and cost-effective performance.

11. ACKNOWLEDGEMENTS

Much of the work presented in this paper is based on a current research grant from AMIRA. The support of AMIRA and the sponsoring companies is gratefully acknowledged.

REFERENCES

1. Jenike, A.W. "Gravity Flow of Bulk Solids". Bul. 108, The Univ. of Utah, Engn Exp. Station, USA 1961.
2. Jenike, A.W. "Storage and Flow of Solids". Bul. 123, The Univ. of Utah, Engn Exp. Station, USA 1964.
3. Arnold, P.C., McLean, A.G. and Roberts, A.W. "Bulk Solids: Storage, Flow and Handling". The University of Newcastie Research Associates (TUNRA), Australia, 1982.
4. Roberts, A. W ."Modern Concepts in the Design and Engineering of Bulk Solids Handling Systems". TUNRA Bulk Solids Research, The University of Newcastle, Australia, 1988.
5. Thomson F.M. "Storage of Particulate Solids". Chapter 9, Handbook on Powder Science & Technology. (1984) Van Nostrand.
6. Jenike, A.W. "A Theory of Flow of Particulate Solids in Converging and Diverging Channels Based on a Conical Yield Function". Powder Tech., Vol.50. (pp. 229-236).
7. Benink, E.J. "Flow and Stress Analysis of Cohesionless Bulk Materials in Silos Related to Codes". Doctoral Thesis, The University of Twente, Enschede, The Netherlands. 1989.
8. Roberts, A.W. and Ooms, M. "Wall Loads in Large Steel and Concrete Bins and Silos due to Eccentric Draw-Down and Other Factors". Proc. 2nd Inti. Conference on 'Design of Silos for Strength and Flow', Powder Advisory Centre, U.K., 1983, (ppI51-170).
9. Ooms, M. and Roberts, A. W ."The Reduction and Control of Flow Pressures in Cracked Grain Silos". Bulk Solids Handling, Vol. 5, No.5, Oct. 1985. (pp.1009-1016).
10. Roberts, A. W. "Some Aspects of Grain Silo Wall Pressure Research -Influence of Moisture Content on Loads Generated and Control of Pressures in Tall Multi-Outiet Silos". Proc. 13th Inti. Powder and Bulk Solids Conf., Chicago, USA, May 1988. (pp.II-24).
11. Australian Standard AS89138 "Loads on Bulk Solids Containers"
12. Roberts A. W ., Ooms M and Manjunath K.S., "Feeder Loads- and Power Requirements in the Controlled Gravity Flow of Bulk Solids from Mass-Flow Bins" Trans. I.E.Aust., Mechanical Engineering, V.ME9, No.1, April 1984.
13. Manjunath,K.S. and Roberts, A.W., 'tWall Pressure-Feeder Load Interactions in Mass-Flow Hopper/Feeder Combinations". Part I. IntI. Jnl. of Bulk Solids Handling, Vol. 6, No.4, Aug. 1986.
14. Manjunath, K.S. and Roberts, A.W., "Wall Pressure-Feeder Load Interactions in Mass-Flow Hopper/Feeder Combinations". Part II. Inti. Jnl. of Bulk Solids Handling, Vol. 6, No.5, Oct. 1986.
15. Rademacher, F.J.C., "Reclaim Power and Geometry of Bin Interfaces in Belt and Apron Feeders". IntI. Jnl. of Bulk Solids Handling, Vol. 2, No.2, June 1982.
16. Roberts, A. W. and Teo, L.H., "Performance Characteristics of Gravity Reclaim Stockpiles of Conical Form", Trans. of Mechanical Engineering, The Instn. of Engrs. Australia, Vol. ME 14, No.2, 1989, pp.97-102.
17. Roberts, A. W .and Teo, L.H., "Design Considerations for Maximum Reclaim Capacity of Conical Stockpiles", IntI. Journal of Bulk Solids Handling, Vol. 10, No. 1, 1990.
18. Ooms, M. and Robens, A.W. "Significant Influence of Wall Friction in the Gravity Flow of Bulk Solids". IntI. Jnl. of Bulk Solids Handling, Vol. 5, No.6, 1985 (pp.1271-1277)
19. Robens, A.W., Ooms, M. and Scott, O.J. "Surface Friction and Wear in the Storage, Gravity Flow and Handling of Bulk Solids". Proc. Conf. 'War on Wear', Wear in the Mining and Mineral Extraction Industry, Instn. of Mech. Engnrs, Nottingham U.K., 1984. (pp.123-134).
20. Robens, A. W. "Friction, Adhesion and Wear in Bulk Materials Handling". Proc., AntiWear 88, The Royal Soc. London. 1988. Inst. of Metals, I.Mech. E. .
21. Roberts. A.W., Ooms, M. and Wiche, S.J. "Concepts of Boundary Friction, Adhesion and Wear in Bulk Solids Handling Operations". IntI. Jnl. of Bulk Solids Handling, Vol.10, No.2, May 1988. :
22. Robens, A.W."Vibrations of Powders and Bulk Solids". Chapter 6, Handbook on Powder Science & Technology. (1984) Van Nostrand.
23. Robens, A.W., Ooms, M. and Scott, O.1. "Influence of Vibrations on the Strength and Boundary Friction Characteristics of Bulk Solids and the Effect on Bin Design". Inti. Jnl. of Bulk Solids Handling, Vol.6, No.1. 1986. (pp.161-169).
24. Robens, A.W. and Rademacher, F.J.C. "Induced Gravity Flow by Mechanical Vibrations". To appear in Inti. Jnl. of Bulk Solids Storage in Silos, UK.
25. Robens A. W. "An Investigation into the Gravity Flow of Non-Cohesive Granular Materials Through Discharge Chutes". Trans. A.S.M.E., Jnl. for Engng. in ,Industry, Vol. 91, Series B, No.2, May 1969. (pp. 373-381). ,
26. Robens A. W. and Scott O.1. "Flow of Bulk Solids Through Transfer Chutes of J Variable Geometry and Profile". Bulk Solids Handling, Vol. 1, No.4, December 1 1981. (pp. 715-727).
27. Parbery , R.D. and Robens, A. W ."On Equivalent Friction for Accelerated Gravity 1 Flow of Granular Materials in Chutes". Powder Technology, Vol. 48. 1986. (pp. 75-79). ;
28. Savage, S.B. "Gravity Flow of Cohesionless Granular Materials in Chute and Channels". J.Fluid Mech. Vol.92, Pan 1, 1979. (pp.53-96).
29. Andrews, B.R., Boundy, B .1. and Roberts, A. W ., "Flow Property Analysis, Design and Construction Details for a 2400 tonne Mass-Flow Bin". IntI. 1nl. of Bulk Solids Handling, Vol. 3, No.4, November 1983. (pp.781-786).
30. Roberts, A. W., " Abrasive Wear Testing and Analysis in Bulk Solids Handling", Report of Bulk Solids Research Group (Sectie Stort-geotechnologie), Dept. of Mechanical Engineering, University of Twente, The Netherlands, 1986.
31. Roberts, A.W., "Hopper and Chute Performance and Wear", AMIRA Project No. 245, Handling of Bulk Solids, The University of Newcastle, 1989.
32. Roberts, A. W., Ooms, M., Askegaard, V. and Wiche, S.1. "Investigation of Flow Instabilities and Beating in Silos'. Paper for Presentation at the cmsA 90 Congress, Prague, Czechoslovakia. August 1990.