An Experimental Technique to Measure Creep in Conveyor Belt Drives
A. Bhaskar Karanth,
K. Ramakoteswara Rao and
M.A. Parameswaran, IndiaSummary
Creep is a phenomenon which is not understood clearly in the context of belt conveyor drives especially in multiple pulley drives. It poses problems in operation such as slipping, wear, varied drive factor etc. To study this phenomenon experimentally, a technique using the reflectivity of material is developed. The relevant circuitry and technique of a pick-up are explained in this paper. The laboratory experimental technique described here can be extended to the actual conveyor.
Nomenclature
B belt width [mm] d distance between two consecutive sensors in a pair [mm] dom distance between two identification marks (lMs) [mm] dos distance between two sensors S1 and S2 at no load [mm] E*d dynamic modulus of elasticity [N/mm] E* modulus of elasticity [N/mm] TE effective tension at drive pulley [N] ToE effective tension at drive pulley (no load) [N] tom time between two lMs at departing point at no load [ms] tos time between two sensors for an IM at no load [ms] tlm time between two lMs at departing point with load [ms] tls time between two sensors for an IM at load [ms] V1, V2 belt velocity at points of approach and departure of a pulley [m/s] Vom belt velocity at reference condition (IM) [m/S] Vlm belt velocity at loaded condition (IM) [m/S].
1. Introduction
The belt conveyor is perhaps the most widely used equipment in transporting bulk solids in various process industries. Essentially it consists of an endless belt running over a set of drive and driven pulleys, supported by idlers in between. There are different types of drives generally used in driving the belt conveyors such as single pulley drive, two pulley drive and multiple pulley drives etc. The conveyor belt drive has the function of transmitting the power to the conveyor belt. The conveyor belt, being a composite with viscoelastic properties, is subjected to changes in length caused by tension variations during operation. This gives rise to the phenomenon of creep. The changes in elongation are not constant due to a variation of the dynamic modulus of elasticity over the working range of the belt conveyor [1,2]. This makes it impossible to predict creep theoretically. Whenever a belt passes over a drive pulley there is a change in belt tension accompanied by a small change in the velocity of the running belt from the approaching point to the departing point of the pulley. This is termed as creep. The variation of creep causes deviations from the traditional calculations carried out with respect to tensions at different drives in a multiple pulley drive system of a conveyor.
2. Previous Works
VIERLING [2] derived a formula to calculate the creep movement. He stated that if the dynamic modulus of elasticity Ed effective angle wrap, angle of wrap, diameter of the pulley D, and stress at the departing point of the drive are known, then the movement of creep can be estimated.
The recommended practice for troughed belt conveyors [3] gave a definition that slip between pulley and belt is termed as creep. According to the definition the creep can be calculated by knowing the belt velocity of approach and belt velocity at departure at drive pulley or effective tension and modulus of elasticity. i.e.
Creep (%) = |
V1 - V
2 |
x 100 |
V1 |
||
= |
TE |
x 100 (1) |
T1 + E
d |
where Ed = B.E*d
SuR [4] has stated that there is a velocity difference at the drive pulley due to the elongation of the belt with load. The elongation in cotton belts is higher than in steel cord belts. The design and operation of the multiple pulley drive system requires a good knowledge of the creep to ensure that the system works as required.
The present work is intended to measure the creep on a belt conveyor drive pulley experimentally. The previous works [2] were purely theoretical. Even to estimate creep theoretically, the effective angle of wrap, coefficient of friction and dynamic modulus of elasticity have to be determined experimentally. Compared with velocity it is quite difficult to obtain these quantities on an actual belt conveyor. A simple and effective method is to estimate the surface speed of the conveyor belt at the approaching and departing points at any drive pulley.
2. Measurement Technique
3.1 Method 1
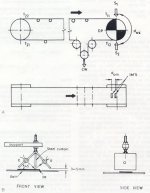
This method is based on material reflectivity. To measure the velocities at different points on the conveyor, infra-red photo pick-ups are used as shown in Fig. 1, where:
S1 - sensor position at approaching point of drive pulley
S2 - sensor position at departing point of drive pulley.
This pick-up senses the evenly spaced identification marks (lMs) from the running conveyor belt. The colours of these 1Ms (yellow, white or light green) contrast with respect to the black belt conveyor.
The pick-up used for this application is an infra-red diode, which emits the infra-red light (emitter), and an infra-red transistor in which the base (receiver) voltage depends upon the infra-red light intensity. The base (receiver) receives reflected rays from the emitting source. The emitter and receiver are mounted on a holder which is made specifically for the purpose. This holder facilitates holding the emitter and receiver at 45 to the conveyor belt as shown in Fig 1. The two are separated by a steel curtain so that there is no chance of unwanted light passing directly from emitter to receiver. Whenever a distinct IM passes below this pick-up, the base (receiver) voltage of the transistor increases and this causes the current to flow between the collector and emitter of the transistor depending upon the intensity of the incidental light.
Fig. 1: Schematic view of the transducer and IM positions
A. Arrangement of pick-ups and lMs in a belt conveyor;
B. Arrangement for fixing pick-ups; E = Emitter; R = RecieverThis voltage can be recorded through a Wave Form Analyzer (WFA) or Analog to Digital Converter (ADC) or a storage oscilloscope with an interfacing circuitry. The block diagram of the circuit used is shown in Fig. 2. This should be suitably modified to suit the recording instrument connected.
Fig. 2: Block diagram of the circuitry developed
The IM can be made with commercially available color adhesive tapes or with paint. The first option has the advantage that the width of lMs remains constant with no trouble.
3.1.1 Decoding of Measured Signal
The signals which are recorded on a time scale are decoded using the appropriate technique. In the present case the WFA is used which gives the time at different positions of the recorded wave by moving the cursor. If an ADC is used then a program is written to find the change in voltage and time between two such changes. These time intervals are used to estimate the velocities at different points as explained later.
3.1.2 Data Required
Width of the identification mark at reference condition, w (mm)
Distance between the two lMs at reference condition, dom (mm)
Difference in reflectivity between conveyor belt and lMs in terms of voltage (mV).
The first two can be measured with sufficient accuracy using a vernier calliper at the reference condition (at no load with take-up tension and stand still). The last one can be found out by focusing the sensor on both materials, one at a time with the belt stationary. The reference signal required is to be recorded at S2 for the same lMs with no load on the belt conveyor (i.e. with the minimum initial tension and close to gravity take-up).
3.1.3 Effect of Belt Elasticity and Motor Speed
Whenever there is an elongation of the conveyor belt due to load, there will be a corresponding elongation of the lMs since they are glued to the conveyor belt. As the lMs are of the same width and glued with the same method, the distance between the centres of the lMs changes. Only the change in this distance is of consequence. Rotational speed (rpm) of the drive changes with load depending upon the drive characteristics, especially in the case of the induction motor, and fluid couplings, in any. This leads to a change in the peripheral speed of the pulley, thus affecting the time required to travel the same distance by a small margin. This change can be corrected by knowing the speed torque characteristics of the drive, but as seen later such a correction is not essential.
3.1.4 Calculation of Velocity
The recording of the time elapsed (tom) to cross over a known distance between lMs (dom) taken at known tension (i.e. at departing end closer to gravity take-up) form the basis for further calculations. The time taken (tos) by the particular lM to cross over from the approaching end sensor (S1) to the departing end sensor (S2), at the above condition is used to calculate the distance between two sensors.
The initial calculations are as follows:
Conveyor with no load:
| Creep = Toe / T1+Ed ≈ Toe / Ed as T1 << Ed | |
| also creep = (V1 - V2) / V1 | |
| Vom = dom / tom = V2 (2) | |
| and V1 = V2/[1 - (Toe/Ed)] (3) | |
| dos = V1 tos + 0.5tos [V1 - V2] (4) | |
The difference between V1 and V2 is very small as the effective tension required is very small when compared to the elastic modulus of the belt at no load. The distance along the arc on the pulley surface between two sensors is not known accurately from physical measurements, but can be calculated from Eq. (4) after estimating the velocities from Eqs. 2 and 3 and then used as a basis for further calculations.
Conveyor with load:
At S2, the distance between the two lMs under consideration is the same as in the case of no load. This is because the tension at this point is not changed due to the fact that the constant tension is maintained at this point by the gravity take-up.
So, the new velocity at S2 is given as follows:
Vlm = V2 = dom/tlm (5)
Due to the contraction of the belt, the velocity at departing point S2 is less than the velocity at approaching point S1. The distance between two sensors (dos) remains the same for all operations. The time (tls) taken by an lM to travel between two sensors is known from the recorded signal. Then substituting the above in Eq. (4) and rearranging the terms to obtain V1:
V1 = (2dos - V2 tls)/ tls (6)
The belt velocity of depart and approach can be calculated for different loads from Eqs. (5) and (6) and hence the creep. in multiple puiley drives the reference velocity should start at the point closer to the gravity take-up.
3.2 Method 2
This method is more accurate than the earlier method as the estimation of the modulus of elasticity of belt and effective tension will lead to small errors as Ed changes with loading and aging of the conveyor belt. A pair of sensors separated by a specific distance is placed such that one is at the point of approach, and similarly another pair is placed such that one is at the point of departure and the other is at a specific distance away in the direction of belt movement.
The time taken for any one lM to travel between a pair of sensors located both at approaching and departing points is recorded separately and velocities are obtained as follows:
V1 = d/t1 and V2 = d/t2
where t1 and t2 are the times taken by the mark to travel between two sensors at approaching and departing points.
3.3 Experimental Authentication
As the first method requires only two pick-ups to measure the creep, measurements are made by this method on the experimental set up which has frictional loading as shown in Fig. 3. The output of the pick-up was connected to the WFA which is able to read and record the signal at an interval of 1 micro second to 64 ms. Fig. 4 shows the signal captured in the WFA from the pick-up at 1 ms without waveform correction.
Fig. 3: General arrangement of the experimental set-up
Sample Calculation by Method 1
Data:
|
E = |
1,240 kN/m |
ToE = |
183 N |
dom = |
500.5 mm |
|
Belt Width = |
400 mm |
tom = |
1,297 ms |
toS = |
1,445 ms |
tlm = |
1,320 ms |
tls = |
1,468 ms |
| Creep calculation: | |
Vom = |
500.5/1,297 |
|
= |
0.3858905 mm/ms |
| Using Eq. (2) | |
Vos = |
0.3858905/(1 - 183/496 * 10) |
|
= |
0.3860329 mm/ms |
dos = |
0.3858905 - 1445 + 0.5 * 1445 |
|
|
[0.3860328 - 0.3858905] |
|
= |
557.7146 mm |
Vlm = |
V2 |
|
= |
500.5/1320 |
|
= |
0.3791666 mm/ms |
V1 = |
(2 * 557.7146 - 0.3791666 * |
|
|
1468)/1468 |
|
= |
0.3806626 mm/ms |
| Creep (%) = | |
|
= |
0.3806626 - 0.379166
* 100 |
0.3806626 |
|
|
= |
0.3930885% |
4. Conclusions
The techniques suggested are reliable in measuring the velocity at approaching and departing points of a drive pulley. The creep can be calculated using simple formulae taking the time elapsed between two points, directly from the data recording. The second method offers a simple way to measure the creep even without knowing the type of the belt and its properties. These techniques can be used for steady state measurement of creep and slip with minimum amount of modifications to the actual systems. They can also be extended to measure starting creep and slip of the conveyor in multiple pulley drives using a multichannel recorder.
Along with precisely measured pulley diameter and rpm, these techniques can be used to cheek the slip between the drive pulley and conveyor belt. They can also be extended to any conveyor with constant load by gluing the 1Ms at the appropriate places where material will not cover them.
References
LANGE, H.: Load distribution with dual pulley belt drive; Frdern und Heben, Vol. 14, No. 9, pp. 677-679.
VIERLING, A.: Zur Theorie der Band Frderung; Continental Transport-band-Dienst, 3rd Edition 8, 1972.
Mechanical Handling Engineer's Association, U.K.: Recommended practice for troughed belt conveyors; London, 1986, p. 56.
SUR, S.: Dual drives for belt conveyors; bulk solids handling Vol. 7 (1987) No. 4, pp. 509-514.
