Courtesy : Trans Tech Publications - Bulk Solids Handling Journal

1. Introduction

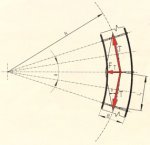
Belt conveyors with horizontal curves have been successfully used for some years, as demonstrated by a variety of existing plants. The belt conveyors in the Power Station Plant Soma, Turkey, (Fig. 1) with a length of 8.5 km, and the 6 km long belt conveyor in the Optimum Coal Mine, South Africa [3], are mentioned as examples. Plans to use conventionally designed belt conveyor systems for ever narrower curves require that basic calculation principles used in the past should now be critically analysed, and that other factors, which were insufficiently considered in the past, should now be taken into account.

Belt conveyor in Soma Power Plant complex [2]

2. Present Status

The development of the theoretical principles for the design of belt conveyors over the course of time can be derived from [5]. Published research up to now has mainly investigated the influence of

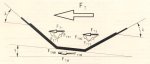
1. a. radiaily acting force components F_GB from deadweight of the belt G_B and its troughability,

2. radially acting force components F_GG from dead-weight of the material G_G and

3. radially acting components F_R from friction force by tilted carrying idlers on the position of the conveyor belt in the horizontal curved (Fig. 2). These forces, with an admissible off-centre belt run, are required to be in balance with the force F_T obtained from the belt tension force T acting radial to the inner side of the curve.

F_T = F_GB + F_GG + F_R              (1)

Fig. 2: Cross-section through a belt conveyor in a horizontal curve, forces and geometry

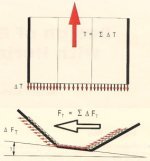
Fig. 3 shows the basic model for calculation of the radial force resulting from the belt tension force with

F_T = T * I_T / R             (2)

Fig. 3: Top view of a belt conveyor in a horizontal curve, forces and geometry

where T is the belt tension force in the relevant section of the belt, I_T the spacing between the carrying idlers and R the radius of the horizontal curve. Past evaluations did not consider that the radial force F_T at the troughed belt has to be split, analogously to the weight forces G_B and G_G, into components vertical and parallel to the carrying idlers to properly determine the effect of this force on the position of the belt.

As far as the normally used horizontal curve radii of conventionally designed belt conveyors is concerned, an approximate approach can be set up assuming the belt tension force T to be uniformly distributed over the total belt cross-section (Fig. 4). As a consequence thereof, the radial force share ΔF_T is in proportion to the width of the belt section in contact with the carrying idlers of the belt trough.

Fig. 4: Distribution of the belt tension force T and the radial force F_T in a horizontal curve over the belt cross-section

The following calculation equations are obtained for the components of the radial force F_T1 , F_TM and F_T2 (Fig. 5)

FT1	SB1	* FT	(3)
	B
FTM	IM	* FT	(4)
	B
FT2	SB2	* FT	(5)
	B

Fig. 5: Model fro distribution of te radial force F_T to individual sections of the belt cross-section

where S_B1 and S_B2 represent the length of the outer carrying idlers in contact with the belt and I_M the length of the center carring idler. The components

F_TN1 = F_T1 * sin(λ + γ)    (6)
F_TNM = F_TM * sinγ           (7)
F_TN2 = F_T2 * sin(λ - γ)     (8)

are acting vertically to the shell surface of the carrying idlers and have to be considered for determination of the friction forces of tilted idlers.

The radial force components

F_TT1 = F_T1 * cos(λ + γ)    (9)
F_TTM = F_TM * cosγ           (10)
F_TT2 = F_T2 * cos(λ - γ)     (11)

act parallel to the carrying idlers and have a direct influence on the position of the belt. Thereby it was considered that the forces parallel to the carrying idlers follow the direction of the belt trough in the case of commonly used troughing angles, this being a consequence of the transverse stiffness of the belt in the transition area between two adjacent carrying idlers. This was supported by experimental investigations [1]

Thus, with F_TT as sum of the components of F_T acting parallel to the carrying idlers,

F_TT = F_TT1 + F_TTM + F_TT2           (12)

the following equation is valid to determine the off-centre belt run

F_TT = F_GB + F_GG + F_R           (13)

Since |F_TT| < |F_T| is valid for a troughed belt, it becomes obvious that past calculation principles started from too high forces acting towards the inner curve. According to [5] the following equation is valid for the determination of F_GB and F_GG