
| Modern Pulley Design Techniques And Failure Analysis Methods |
|
Vinit Sethi and Lawrence K. Nordell
Conveyor Dynamics, Inc.
1111 West Holly Street
Bellingham, WA 98225
Published standards and specifications do not adequately cover engineered class pulleys for modern high strength steel cord belt conveyors. This paper discusses the Conveyor Dynamics, Inc. (CDI) design criteria and stress analysis techniques emphasizing the finite element method (FEM), fatigue failure criteria, design limits and manufacturing requirements to ensure successful and safe pulley installations.
INTRODUCTION
High tension engineered class pulley applications are exceeding conventional wisdom including published industrial and academic guidelines. Since they are not covered by standards or manufacturer's published information, and require custom engineering, they are classified as "engineered class'. Installations beyond 6000 kW (8000 HP) are becoming commonplace. The cost of a catastrophic failure in this power range can have grave consequences on personnel safety and on the plants profit and loss statement. Unfortunately, no industrial committees, government bodies, academic or technical societies have taken a leadership role to set forth appropriate instruments to manage the diversity of opinions in this field. Manufacturers differ on the following criteria:
types of stresses that are important,
fatigue stress range criteria,
allowable stress limits in welded and non-welded members,
allowable load limits on the pulley components,
material surface finish criteria in critically stressed areas,
analytical tools that resolve the necessary stress factors,
materials of construction and their limitations,
fabrication techniques, constructed tolerances and tolerance controls,
quality assurance definitions and practices,
guidelines for cold weather conditions,
appropriate lagging specifications.
Engineered class pulleys are defined as those which fall into any of the following categories:
Shaft diameter exceeding 250 mm (10 in.)
Steel cord belt applications
Pulley face width exceeds 1675 mm (66 in.)
Pulley diameter exceeds 1500 mm (60 in.)
Pulley load exceeds 30,000 kg (66,000 lbs.)
Belt modulus exceeds 8000 N/mm (48000 lbf/in)
Bikon, Ringfeder or other nonstandard connections
Stub shaft pulleys
Not covered by American National Standards Institute (ANSI) No. B105.1
This paper will attempt to address some of these issues with the introduction of some of CDI's design and stress criteria, and pulley stress analysis techniques for steel drum pulleys.
DESCRIPTION OF PULLEY COMPONENTS
The main components of a pulley for a conveyor belt application are shown in Figure 1.

Figure 1. CROSS-SECTION OF PULLEY ASSEMBLY
Shell: The belt is wrapped around the shell surface. The shell is usually constructed by rolling a single flat plate into a cylindrical shape or by forming two half cylinders in a press. The shell or rim can be a plate rolled equal to the pulley face width or in a shorter central shell body, which is attached to a rim section machined integral with the end-disk as shown in Figure 1. Run-out tolerances and metal distortions are controlled by machining the shell and line boring the hub after all welding and stress relieving are completed.
End-disk And Hub Assembly: End-disks and hub assemblies of many different shapes have been used. They can be a straight plate, tapered, curved or turbine, pencil. shaped etc. as illustrated in Figure 2.

Figure 2. DIFFERENT END-DISK GEOMETRIES
The end-disks can be made of cold rolled plate, casting, forging, machined plate or fabricated pieces. The turbine shape reduces the disk stiffness while optimizing the distribution of end-disk bending stresses. At a given end-disk cross-section, the sign () of the bending stress alternates from the hub to the shell, as shown in Figure 3. The profiled or turbine end-disk takes advantage of the bending stress crossing through zero. Near this point, the end-disk, metal thickness can be significantly reduced without adversely affecting the end-disk load capacity. In effect, the optimal profiled or turbine shape closely follows the magnitude of the bending stress. Contact stresses at the connection of the locking device with the shaft and the hub are reduced by the increased flexibility. In addition, a smaller locking mechanism may be used due to the reduced end-disk moment.
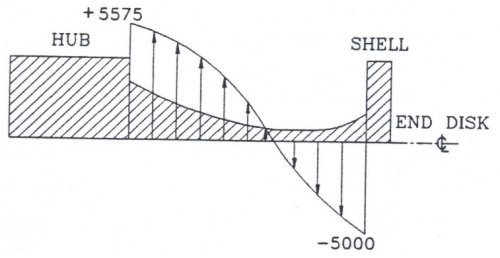
Figure 3. BENDING STRESS DISTRIBUTION OF END-DISK CROSS SECTION
The most common types of end-disk construction are shown in Figure 4. Figure 4a shows a pulley with a plate type end-disk that is welded to both the shell and the hub. Large alternating bending stresses combined with possible weld inclusions, high stress risers in welded surfaces, and other flaws in the hub/end-disk make it a questionable design. All welded sections have reduced metal fatigue strength as will be described later. Weld zones in pulleys are inherently more failure prone. Therefore, for engineered class pulleys, Figure 4b shows that welding is minimized by integrating the hub and turbine shaped end-disk from a common metal plate. Figure 4c shows the shell outer section is incorporated into the hub-end-disk from a single metal form in more advanced designs. This eliminates all fillet welds. Fillet welds have a significantly lower allowable fatigue stress range than does native metal, typically 33% [British Standard BS5400 Part 10, 19801 of the metal's fatigue rating. The end-disk hub to disk fillet welds are subjected to usually compressive alternating stresses due to the locking device expansion. The absence of tensile stresses reduces the likelihood of crack propagation. Alternative designs such as the one shown in Figure 2e are being investigated as cost effective alternatives, due to the reduced machining requirements.
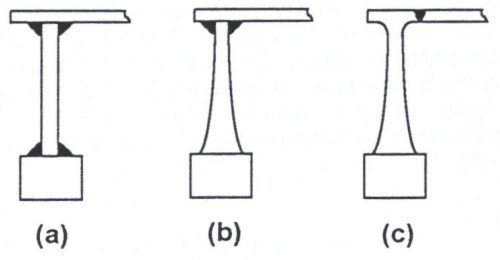
Figure 4. DIFFERENT TYPES OF END-DISK WELD CONSTRUCTION
Locking Mechanism: Engineered class pulley assemblies are typically fastened to the supporting shaft with a non-keyed locking device. The non-keyed locking device uses pressure and friction to secure the pulley to its shaft. This eliminates the keyway and its stress risers, thereby increasing the shafts load capacity, by as much as 60% [Bikon Locking Assemblies Catalog].
Bikon and Ringfeder are manufacturers of the two most commonly used friction-style locking mechanisms for conveyor pulley applications. The Bikon (Figure 5) or Ringfeder style locking mechanisms use the wedge principle to translate clamp loads from locking screws into radial contact pressures on the shaft and hub bore creating a mechanical interference fit. These devices can be easily installed or removed, can transmit high torques, thrust loads and bending moments. There is however a stress concentration created at the edge of a locking device due to notch effects created by the locking pressure, shaft bending moment, and reaction to the resultant belt forces. This can be reduced by the use of a raised journal on the shaft on which the locking device will sit. The raised journal extends about 1 mm (0.040 inches) above the shaft with generous fillet radii, Its length is 1-2mm (0.040-0.080 inches) less than the locking device collar. The purpose is to allow the locking device edge to plastically deform the edge at the shaft raised journal. This produces a more uniform load pattern across the shaft contact zone similar to crowning cylindrical rollers of a modern bearing assembly. The raised section can be eliminated if the locking mechanism manufacturers provide appropriate corner radii.
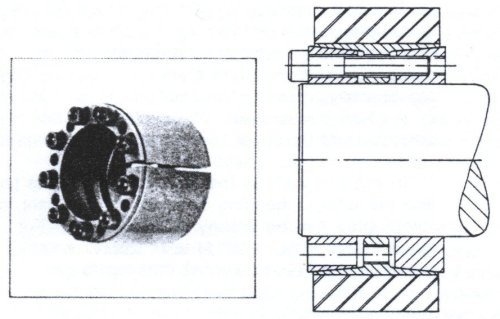
Figure 5. SCHEMATIC OF LOCKING MECHANISM
In 1985, a high capacity conveyor (2800 kW) take-up pulley failed after about three months of service. Our investigation reported that a combination of a stiff end-disk and flexible locking device caused a high local stress riser on the shaft that caused the fatigue failure. The failed pulley is shown in Figure 6. The CDI locking device selection criteria were formulated from this failure data.
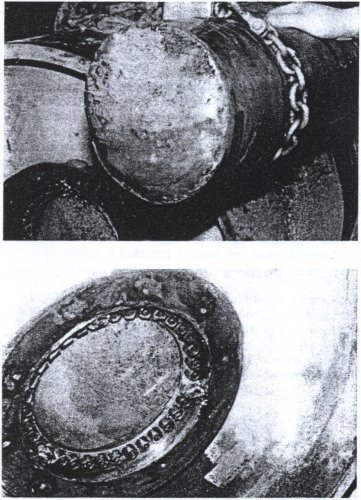
Figure 6 SHAFT FATIGUE FAILURE AT LOCKING DEVICE SHOULDER
In 1986, a large 2600 kW (3500 hp) downhill conveyor was analyzed using the CDI criteria The conveyor had been in operation for about two years. We reported to the client that the design was theoretically in danger of a catastrophic fatigue shaft failure. The client investigated the pulley and found our assessment to be true. The pulley assembly was removed from service and rebuilt using a wider locking device which significantly reduced the locking device edge stress. Similar findings have been made on other conveyor systems.
Shaft: Pulley shafts are subjected to a combination of bending stresses due to the belt loading, torsional stresses from motor driving torque and high local contact pressure due to the compressive action of the locking mechanism. Drives with shaft mounted reducer/motor assemblies can impose additional bending forces which are superimposed on the basic forces. The extent of shaft bending is dependent on the flexibility of the end-disks and its locking device and on the shaft sectional modulus. If the locking device and end-disks are quite stiff, then the shaft will bend mainly outside of the pulley. Highly flexible end-disk arid locking device assemblies require a stiff, high sectional modulus shaft, between the pulley end-disks, to gain design economy. Some manufacturers use a secondary internal shell or drum (double drum) to increase the apparent shaft sectional modulus. We do not recommend this procedure for shafts over 300 mm (12 in.) diameter. The weld connection of this extra drum to the end-disk hub presents design problems which have not been solved to date (i.e. more capacity is assumed than can be achieved). We find that the extra drum cannot deliver all of the extra sectional modulus inherent in the secondary drum's cross-section. The end-disk then becomes overstressed at the hub connection leading to observed fatigue failure of the end-disk.
Stub shaft studies are in progress to develop special stiff end-disk designs that will provide better economy and/or better shipping, handling, erection and maintenance of large pulley systems. A number of designs are in review. Two concepts are illustrated in Figure 7.

Figure 7. STUB SHAFT PULLEY DESIGNS
Lagging: Lagging is a covering that is applied to the surface of the shell to improve performance in certain applications. In the case of a drive pulley, the use of lagging can increase the coefficient of friction between the belt and the pulley preventing slipping even with lower belt tensions. Lagging reduces rapid shell wear in mining applications involving abrasive materials like iron ore. Lagging is usually made of an elastomer or ceramic. The lagging can have different patterns depending on the application. The herring-bone or diamond groove patterns are used for their ability to allow water to escape in wet applications. CDI recommends the diamond pattern because of its superior compression characteristic. Other patterns are used to improve belt-tracking. The depth and spacing of grooving have taken many forms. The specifications are dependent on applications. A discussion on sizes and pattern of grooving, and material properties requires more discussion than can be provided in this paper.
Recently, two large conveyor systems (4500 kW and 7100 kW) suffered from lagging damage. Review of international literature, internal investigation and material testing showed that existing hot vulcanizing material specifications and grooving patterns must be upgraded. In the case of the above noted conveyors, cold bonded lagging was successfully applied in place. The tensile strength, tear strength, and abrasive index are superior with the new cold bonded lagging, and with special polyurethane lagging, than with today's conventional hot vulcanized lagging.
Ceramic lagging has shown benefit with increased friction and wear resistance. Insufficient data exists to recommend its use in drive pulleys above 3000 kW.
CONVEYOR DYNAMICS, INC. DESIGN CRITERIA
CDI has established certain stress and manufacturing criteria with which to compare and evaluate various pulley designs with respect to risk-free long term operation. The stress criteria comprise of static and fatigue strength analyses. These stress criteria consist of setting limits on both the maximum stresses and on the stress range that can occur in different components of the pulley (shell, disk, hub and shaft). The three dimensional stress field consists of radial, tangential and axial stresses, which are analyzed in the pulley.
Static Strength Criteria
While evaluating ductile materials, yield strength of the material is usually used as the failure criteria In the case of brittle materials, like cast iron, which do not have a yield point, the ultimate strength of the material is used as the failure criteria. CDI uses the Distortion Energy Theory [Shigley, J.E., 1986] for performing static strength analyses. This theory is meant for ductile materials as it predicts the initiation of yield.
The Von Mise's stress 0e is used in the theory. For a triaxial stress state, the Von Mises stress is defined in terms of the principal stresses 01, 02 and 03 as:
σe = [0.5* {(σ1 - σ2)2 + (σ2 - σ3)2 + (σ3 - σ1)2}]0.5
Principal stresses a~. a2 and 03 are normal stresses that act on planes that do not carry any shear stress. Maximum and minimum principal stresses act on mutually perpendicular planes, and are the algebraically largest and algebraically smallest normal stresses to be found at a paint in a given stress field. These stresses are not to be confused with the radial, tangential and axial stresses.
In regions such as the shell where only the tangential and the axial or bending stresses are dominant, a biaxial stress state can be assumed for simplicity. For a biaxial stress state, the Von Mise's stress is obtained by substituting 03=0 in the above equation to get:
σe = [0.5* {(σ12 - σ1σ2 + σ22]0.5
According to this theory, yielding occurs when the Von Mises stress equals the yield stress. Experiments have shown that the distortion-energy theory predicts yield with the greatest accuracy amongst the accepted stress theories. The CDI criteria uses the Distortion Energy theory with a multiplier of 0.7 which accounts for probabilistic conditions such as variations in metallurgy, metal porosity, inclusions, and other uncertain conditions. This multiplier of 0.7 is slightly higher than the 0.6 to 0.66 multiplier used for welded structures [Shigley, J.E., 1986]. Thus the maximum acceptable Von Mise's stress in the shaft, end-disk and shell is (0.7 X yield stress of the component).
Fatigue Strength Criteria
In the case of most pulleys, the largest range stresses in the shell are usually in the tangential or hoop direction and occur close to the centerline of the pulley. Pulleys with wide shell faces may have the largest range stress in the axial direction due to bending in a region close to the shell/disk connection. The British Standard BS5400 Part 10 is used to determine the allowable stress ranges for the circumferential and seam welds in the shell for infinite fatigue life as shown in Figure B.

Figure 8. CIRCUMFERENTIAL AND AXIAL WELD CLASSIFICATIONS
Shell Circumferential Welds have an allowable axial stress range of 77 MPa (11165 psi) (Class C weld) and allowable hoop stress range of 100 MPa (14500 psi) (Class B weld). These values apply if the welds are full penetration and have been ground flush and proven free of defects. If they are not ground flush and proven free of defects, the allowable axial stress range reduces to 55 Mpa (7975 psi) (Class D weld) and the hoop stress range to 77 MPa (11165 Ps) (Class C weld).
Shell Axial Seam Welds have an allowable axial stress range of 100 MPa (14500 psi) (Class B weld) and hoop stress range of 77 MPa (11165 psi) (Class C weld) if they are full penetration and have been ground flush and proven free of defects. If not, the allowable axial stress range reduces to 77 MPa (11165 psi) (Class C weld) and hoop stress range to 55 MPa (7975 psi) (Class D weld).
These allowable stress ranges are for 10 million load cycles with a 97% confidence level. Radiographic and/or a full ultrasonic inspection must be performed to evaluate the welds.
Disk: For most pulleys, the largest fluctuating or range stresses in the disk are in the radial direction and are due to end-disk bending. The fatigue strength criteria used here is that the maximum stress should not exceed the endurance stress, Se, for infinite life. The endurance stress, 5e~ is dependant on numerous factors including material type, surface finish, stress concentration effects, type of loading, failure mode, etc. A conservative endurance stress of 40% of yield stress (20% for shear) is used for ductile materials to account for the following possibilities, some of which are difficult to quantify:
Unlimited number of starts and stops
Dynamic loads
Irregularities in lagging thickness
Material buildup
Overloading of the conveyor
Shaft: As the pulley rotates, the shaft contact pressure under the locking device changes at the inside and outside shoulders. The alternating stress introduced due to this can lead to fatigue failure if the range is large. Therefore limits are placed on how large this range stress can be, This range stress should not exceed the limits imposed in the modified Goodman diagram as shown in Figure 9.
The modified Goodman diagram can be constructed to define the safe operating envelope for end-disk and shaft stresses. The maximum and minimum values of all stress components at a given point must lie within the envelope defined by the dark lines to be acceptable from a fatigue life standpoint. The envelope can be defined using the following equations:
Given:
σu: Ultimate tensile stress of material
σs: Yield stress
Se: Endurance stress
σmax: Maximum calculated stress (radial, tangential, axial)
σmin: Minimum calculated stress (radial, tangential, axial)
σmean: Mean stress = (σmax + σmin)/2Allowable stress range for 0 < σmean < σyield is given by:
σmax < σmean * (σ - Se)/σu + Se
σmin> σmean * (σu + Se)/σu - SeIf σmean < 0, then σmean - Se < σ < σmean + Se
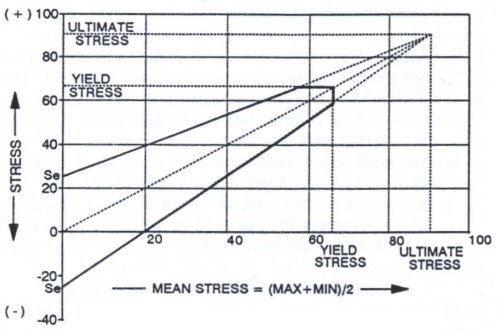
Figure 9. MODIFIED GOODMAN DIAGRAM
Table 1 shows a design evaluation of two sample pulleys using the above static strength and fatigue failure criteria The shaft, end-disk and shell have been evaluated in different sections with both the allowable limits and the calculated stresses listed. Such an approach provides a comparison of different pulley designs with the objective being to determine the best design for an application. The stresses were calculated using programs developed at CDI that are described later.
| Design | #1 | #2 | |
| Locking Device | BIK 1015 | RFN 7012 | |
|
SHAFT |
|||
| Ultimate Stress | 158000 | 120381 | |
| Yield Stress | 135000 | 89923 | |
| Nominal Locking Device Pressure | 27010 | 19200 | |
| a. | Maximum Locking Device Pressure | ||
| Criteria: < (Yield) | 135000 | 89923 | |
| Calculated | 33514 | 35596 | |
| b. | Minimum Locking Device Pressure | ||
| Criteria: > 10% (R) / 2% (S) of Nominal | 2701 | 1920 | |
| Calculated | 20504 | 2804 | |
| c. | Range = (Maximum - Minimum) | ||
| Criteria: < (0.4 x Yield) | 54000 | 35969 | |
| Calculated | 13008 | 32792 | |
| d. | Goodman Fatigue Limit < 1.0 | 0.29 | 1.08 |
| e. | Bending Moment Capacity = (Bending Moment / Tors. Capacity)*100 (%) | ||
| Torsional Capacity | 501900 | 270514 | |
| Calculated Disk Bending Moment | 71608 | 56152 | |
| Criteria: < 32% (1015) / 44.5% (RFN
7015) / 19.5% (RFN 7012) |
< 32
BIK |
<
19.5 RFN < 44.5 RFN |
|
| Calculated | 14 | 21 | |
| Acceptable / Not Acceptable | Yes | No (e) | |
|
END-DISK |
|||
| Ultimate Stress | 90000 | 89923 | |
| Yield Stress ( > 36000 PSI) | 60000 | 40191 | |
| a. | Maximum Von Mises Stress | ||
| Criteria: < (0.7 x Yield) | 42000 | 42134 | |
| Calculated | 34712 | 15204 | |
| b. | Maximum Shear Stress | ||
| Criteria: < (0.5 x Yield) | 30000 | 30096 | |
| Calculated | 20006 | 8737 | |
| c. | Maximum Range Stress | ||
| Criteria: < (0.4 x Yield) | 24000 | 24076 | |
| Calculated (Max. = Radial) | 15419 | 14091 | |
| d. | Goodman Fatigue Limit < 1.0 | 0.73 | 0.59 |
| Acceptable / Not Acceptable | Yes | Yes | |
|
SHELL |
|||
| Yield Stress ( > 3600 PSI) | 50000 | 43511 | |
| a. | Maximum Von Mises Stress | ||
| Criteria: < (0.7 x Yield) | 35000 | 30458 | |
| Calculated | 8882 | 8882 | |
| b. | Maximum Shear Stress | ||
| Criteria: < (0.5 x Yield) | 25000 | 21756 | |
| Calculated | 5128 | 5128 | |
| c. | Maximum Range Stress | ||
| Criteria: < 14500 (R) / 21750 (S) | 14500 | 14500 | |
| Calculated (Max. = Hoop) | 9964 | 9964 | |
| Acceptable / Not Acceptable | Yes | Yes | |
Table 1 SAMPLE EVALUATION OF ALTERNATIVE PULLEY DESIGNS
Manufacturing Criteria
Shell: The shell outside diameter should be machined with respect to its bearing journals within 0.75 mm (0.030 inches) T.I.R. (Total Indicator Reading) for non-drive pulleys, and 0.50 mm (0.020 inches) T.I.R. for driven pulleys. These tolerances minimize excessive local stresses in the steel cord belt splice due to eccentric action and load changes of the motor from the variation in belt speed. With drive pulleys, a snub pulley or second drive is usually located close by where the variation in tolerances can interact. To illustrate this sensitivity the following example is given:
Drive pulley diameter
1000 mm (39.37 inches)
Drive motor electrical slip
1.5% @ 100% torque
Drive & Snub diameter tolerance
0.50 mm (0.020 inches)
Therefore, the diameter variation between drive pulleys can be (0.50 + 0.50) 1.0 mm (0.040 inches). The fluctuation in their belt surface speeds is in proportion to their difference in diameters, causing a number of reactions which follow the speed change. This results in a motor torque fluctuation of 7% (1 mm I 1000 mm x 100% torque / .015 slip = 6.67%), and belt line related stress conditions. Pulley lagging anomalies are additive to this increase. With similar tolerance deviation on the lagging the motor torque fluctuation would also double. This produces added stresses on the shell.
Belt misalignment produces asymmetric forces on the pulley. Maximum acceptable belt misalignment, about 6% of its width, can produce about a 10% increase in the bearing reaction on one side. This increase added to the manufacturing tolerance, noted above, necessitates an equivalent belt line force increase of 10%.
The shell should have a near uniform plate thickness after machining. Our criterion is no more than a 10% difference between minimum and maximum thickness. The minimum thickness should meet the stress criterion. This criterion is set to control the step deviation between the end-disk rim section, which has been machined, and the rolled or formed main shell body, as shown in Figure 3c. We further required the inside circumferential weld be ground flush and tapered smooth at least one full metal thickness beyond the weld in both directions, as shown in Figure 10.
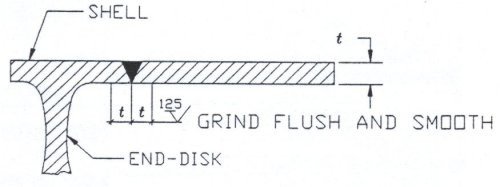
Figure 10. FINISH CRITERIA OF SHELL CIRCUMFERENTIAL WELD
The illustrations below in Figure 11 demonstrate the type of failure which resulted from a step between end-disk and inner rolled shell that was not correctly finished.
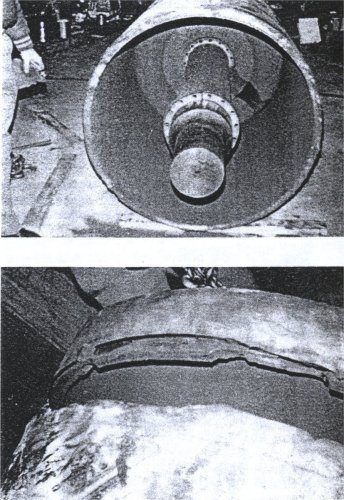
Figure 11. SHELL FATIGUE FAILURE AT DISK/SHELL CIRCUMFERENTIAL WELD
No interior shell stiffeners are allowed on final assembly. Any use of stiffeners during fabrication must be removed. Some manufacturers claim that the stiffeners give the shell added strength. In theory, under some circumstances, this is true, provided full penetration welds are made for the complete circumference on both sides of the stiffening ring. No manufacturer can demonstrate through rigorous analysis that the methods used come close to meeting acceptable criteria (i.e. incorporating proper theory and accepted welding standards). Therefore, the stiffener rings should be lightly welded for later removal and ground finishing. Historically, a number of pulleys have failed along these stiffeners. The manufacturers have reduced the shell stress allowance to compensate for making the ring thicker.
Balancing weights are not permitted on the shell interior between the end-disks. These result in high local stress risers which lead to shell failure. This was recently witnessed on a large belt feeder pulley in Chile. CDI recommends the balance weights be fastened to the shell inside diameter extension outside of the end disk. The weights must not be fastened or welded on the fillet radius region.
End-disk and Hub Assembly: End-disk design is often described as "flexible" or "rigid". The terms refer to the end-disk thickness required to meet the acceptable combined stress level shown in Figure 12.

Figure 12. END-DISK STRESSES VS. PLATE THICKNESS
It is prudent to design a flexible end-disk, if all hub design criteria can be met. The size of welds is then minimized. The locking device bending moment magnitude is minimized and shaft contact stress is minimized.
The end-disk hub size is often specified larger than necessary. the hub contains the locking device. The locking device force expands the hub, which in turn expands the end-disk and rim. Using classical Lam equations and FEM, it can be shown that the end-disk and rim provide considerable restraint on the hub's expansion. Therefore, the analysis should include the end-disk and shell stiffness in the hub analysis. the hub stresses are not allowed to exceed the Von Mises yield criterion.
End-disk connection at the hub and shell should have ample fillet radii. Fillet radii should equal the metal thickness at the respective connections. The fillet radii should have a metal finish of 63 RMS (micro inches) whether welded or machined. The general metal finish outside the fillets is specified to equal or exceed 125 RMS.
The end-disk weld termination , shown in Figure 4a, requires full length welding on the inside and outside of the end-disk, Welding only from the outside produces a significant stress riser at the root of the weld. We have observed a number of shell failures due to this condition.
The end-disk hub should be bored after welding and stress relieving. The shaft should then be mounted, if possible, and the final machining completed on the shell.
The balancing weights should not be welded to the end disk. They may produce unacceptable stress risers and reduced end-disk load capacity.
Locking Mechanism: The Bikon (et. al.) style locking mechanism adds significantly to the flexibility of the end-disk, The manufacturers do not publish the elastic spring constants of their locking devices. Therefore, a theoretical approach is required. The same theoretical principles used to analyze the end-disk and hub have been applied to the locking device. Using thick-wall theory, narrow and wide locking mechanism behavior is incorporated in the CDI analysis. Narrow locking mechanisms (Bikon 4000 and Ringfeder 7012 series) can contribute over 50% of the end-disk flexibility. Wide locking mechanisms (Bikon 1012; 1015 and Ringfeder 7015 series) normally contribute 10-30% of the end-disk flexibility. Seven criteria govern the CDI selection of the most appropriate locking device in combination with the other pulley dimensions:
Transmission of twice motor nameplate torque connected to the driven side of pulley.
Transmission of bending moment, between shaft and end-disk, is given as a function of locking device torsional capacity and is rated by the manufacturers (i.e. Bikon 4000 series <22%, 1015 series <32% 1012 series <35%, and Ringfeder for all series in published tables range from 16% to 60%). Bikon allows momentary loads up to 70%.
Minimum pressure under the locking device must exceed 10% of nominal pressure for normal running forces, and 2% of nominal pressure for momentary overloads (i.e. staffing). This protects against fretting corrosion.
Maximum shaft pressure must not exceed the Von Mises yield criterion as noted in this paper.
Shaft pressure combination of mean and alternating stress cannot exceed Goodman criteria as noted in this paper in Figure 9.
The bolt torque should exceed 75% of the catalog rating for non-driven pulleys.
The locking device inner ring load capacity should be verified by the manufacturer.
Shafting: The shafting should have an overall surface finish exceeding 250 RMS. All surfaces should be finished "bright," removing all scale and surface flaws.
All fillet radii should be finished to 63 RMS.
The locking mechanism journal should be finished at 125 RMS for optimal clamping effect. A finer finish reduces the surface asperity. It is theorized that the reduced asperity causes the mounting lubricants to be trapped as the clamping action is applied, thereby reducing the effective friction. A coarse finish of 250 RMS and higher makes it more difficult to control manufacturing tolerances.
Locking device journal dimensions were mentioned earlier. The fillet radii should exceed the journal step by at least a factor of three.
Many design criteria refer to the shaft deflection limitations. The deflection refers to the angle made by the loaded shaft off its neutral unloaded centerline at the pulley end-disk centerline. It is normally expressed in a dimensionless slope or tangent of the angle. The typical value of the slope for engineered class pulleys is 0.0015. The value is quoted as a free shaft deflection without end-disk assembly restraint. The value originally was derived in practice. This was the value found where the pulley tapered bushing (locking device) would not walk or move on its shaft. The criterion stated in the "Locking Mechanism" section is usually more stringent, It also is more relevant to the locking mechanism design.
All shaft steps or turndown sections from the pulley hub diameter to bearing journal diameter have fillet radii in the step transition sized to control the stress risers. The CDI criterion for stress risers is based on the published work 'Stress Concentration Factors" by R. E. Peterson (1974).
STRESS ANALYSIS TECHNIQUES
Finite Element Method (FEM) Based Methods
Description: The finite element technique has been successfully used to design and analyze conveyor belt pulleys. One of the commonly used references of this application is by L Lindner (1975). A CDI pulley stress analysis program has been developed based on the ANSYS finite element solver, Version 4.4A [Swanson Analysis Systems, Inc., 1989]. This program is fully parametric and can handle most pulley designs and loadings. An axisymmetric geometry is modeled with non-axisymmetric loading to conform with the non-axisymmetric belt tensions. The effect of the locking device expansion is included in the analysis. The nominal locking pressure at the hub is provided as an input to the program along with the belt tensions, orientation of the belt tension vectors and pulley geometry. A variety of end-disk designs can be modeled. These capabilities have been added over a period of time and the program continues to grow in its capabilities. The end-disks that can be modeled include straight, straight tapered, curved, double curved and splines. Flat and tapered hubs can be modeled and so can stepped and straight shafts. Once the input file has been entered, the ANSYS program generates the geometry, meshes it with a mixture of quadrilateral and triangular elements having mid-sided nodes. A sample of the type of mesh structure used in the analysis is shown in Figure 13.
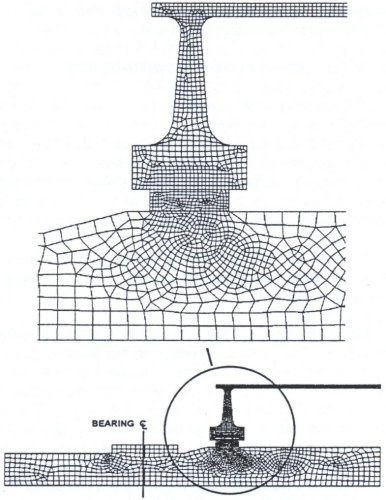
Figure 13. QUADRANT SECTION - FINITE ELEMENT MESH
The non-axisymmetric loading is modeled with a combination of Fourier terms. The program runs each case with one Fourier term and then superposes the solution together to arrive at the composite solution. Overhung loads can also be accounted for in the finite element analysis. A Fourier loading is also used to model the overhung loads.
Selection of number of Fourier terms: The errors associated with approximation in an axisymmetric analysis are introduced in the approximation of the applied loading on the pulley with a Fourier series. Since the solution time is almost directly proportional to the number of Fourier terms in the series, it was necessary to perform an investigation into the influence of number of Fourier terms on the solution. An increase in the number of Fourier terms used to model the loading leads to an increase in the accuracy with which the applied loading matches the desired loading. However, there is a point after which the large increase in solution time outweighs the small incremental increase in accuracy. It was found that for wrap angles of close to 180 degrees, the increase in accuracy in going from 15 Fourier terms to 35 is marginal (less than 1%). This is shown in Figure 14. With wrap angles less than 20 degrees, more than 35 Fourier terms are required to maintain the same level of accuracy.
Figure 14. EFFECT OF NUMBER OF FOURIER TERMS ON LOADING APPROXIMATION
Output from the Finite Element Analysis Program: The output from the program consists of a variety of stress plots of the entire quadrant section or of any subset of that A visual representation of the maximum, minimum and range stresses can be obtained in the form of colored contour plots. A sample plot of the maximum Von Mise's stress is shown in Figure 15. This is a black and white rendition of a color contour plot and this makes some of the stress contours difficult to discern. Additionally, it is possible to generate XY plots which show the variation in a particular stress component at a specific location as the pulley rotates. The program also generates plots of the deformed geometry as the pulley rotates. These are often very useful in determining the cause for a type of stress distribution. Figures 16a-d show the deformed shape of a pulley. This pulley had a 180 degree belt wrap angle which started at 90 degrees and extended to 270 degrees as shown in Figure 16a The scale of the deformations has been exaggerated. Figure 1 6a is at 0 degrees (i.e. outside of the wrap region). The shaft bending due to the resultant belt tensions is maximum at 0 and 180 degrees. It is minimum at 90 degrees and 270 degrees. The shell starts bending inwards due to the belt loading from about 85 degrees and finally bends outwards after the pulley comes out of the wrap region at about 275 degrees.
Classical Mechanics Approach - PSTRESS
Description: PSTRESS is a proprietary program developed at CDI, in 1984, that uses a close-form approximate analytical method to solve for the stresses in a pulley. This program is based on the work of H. Lange (1963) and W. Schmoltzi (1974). The theoretical treatment of the locking device and its reaction into the end-disk, rim and shaft are unique. Thin shell theory is used in the analysis of the shell. The dimensions of the shell, end-disk, hub, locking device and shaft along with the belt tension loads and locking device pressures are input to the program. It calculates stresses including range stresses that can be used for fatigue analysis at various locations that are provided as input to the program. Two Fourier approximations are used to describe the loading on the pulley. One Fourier series is used to describe the loading in the tangential direction while a second Fourier series is used to approximate the loading distribution in the axial direction. The advantages of this program include its ease of use coupled with a short execution time making it a valuable design tool allowing the designer to review the effect of a design change on the stress distribution in a short period of time. Its limitations include a restricted class of end-disk designs that can be analyzed and loss of accuracy at certain locations such as the end-disk / shell connection due to certain assumptions that had to made there to make the analytical solution feasible. CDI is presently in the process of developing a new analytical pulley stress analysis program which will not be restricted by the limitations of the existing program.
Comparison of FEM and PSTRESS results for a pulley: A test case pulley is presented using both, the finite element program and the CDI classical mechanics program PSTRESS. The objective is to demonstrate agreement of the stresses calculated by the two approaches shown in Figure 17. The location selected is the outside of the shell at the pulley centerline. This is usually the point of maximum shell stress. The shell and end-disk connection, and the stresses in the end-disk are also in reasonable agreement.
Figure 17. COMPARISON BETWEEN FINITE ELEMENT ANALYSIS AND PSTRESS RESULTS
EXPERIMENTAL METHODS
Description: Experimental methods used by CDI to measure the stresses in pulleys in operation involve the installation of strain gages at various locations of interest on the pulley. For measurement of stresses on the inside of the pulley, i.e. on the shell, shaft and end-disk, the strain gages must be installed before the installation of the pulley on a shaft. Once the pulley is put into operation, the strain gages will indicate the total strain range at the location where they are bonded. Radio telemetry is used to get the strain data from the rotating pulley into a IBM PC based data acquisition system. Battery powered transmitters are mounted on the pulley. These transmitters modulate the output strain signal from the Wheatstone bridge with a FM carrier wave and transmit it to a sensitive signal conditioning/receiver unit which extracts the strain signal and feeds it to the data acquisition system. Calibration of the strain gages is performed by using a shunt resistance and measuring the output voltage from the Wheatstone bridge.
Comparison of experimental results and FEM for test pulley: An operating pulley was instrumented at the Cordero Mine in Wyoming. It was tested in conjunction with the manufacturer, Precision Pulley, using the procedure described above. Strains at two locations were measured and the corresponding stresses calculated. One of the strain gages was located on the shaft in the interior of the pulley by the manufacturer before it was mounted on a shaft. The other was mounted on the outside of the end-disk. The strain gages were calibrated by introducing a known resistance change along one arm of a Wheatstone bridge circuit. The stress range that the change in resistance corresponded to was calculated. The voltage change produced by the resistance change was recorded, as shown in Figure 18. This provided a correlation between voltage and stress. The purpose of these measurements was to obtain actual stress information with which to compare stresses predicted by the FEM. Figure 19 shows the measured axial stresses in the shaft and the radial stresses in the disk as the pulley is rotating. The axial stress range at the shaft location was measured to be 12.7 MPa (1836 psi). The disk radial stress range was 8.3 MPa (1200 psi). From the estimated belt tonnage, the finite element analysis predicted the axial stress range at the shaft location to be 13.8 MPa (2000 psi) (Figure 20) and the radial stress range at the disk to be 9.2 MPa (1330 psi) (Figure 21). The absolute magnitudes of the predicted values are within 10% of the measured values. The ratios of axial to radial stresses are within 2% of measured values. The exact tonnage on the conveyor during the test could not be obtained and this could account for the error, It was also possible to determine the overload during a loaded startup from the radial stress measurements as shown in Figure 22. The figure shows that the peak stress range during staffing is 156% of the running stress range.
|
Figure 18. STRAIN GAGE CALIBRATION |
Figure 19. STRESSES MEASURED ON TEST PULLEY |
|
Figure 20. FINITE ELEMENT ANALYSIS |
Figure 21. FINITE ELEMENT ANALYSIS |
Figure 22. STRESSES MEASURED ON TEST PULLEY DURING LOADED STARTUP
CONCLUSIONS
CDI is an independent engineering consulting company. We have been successfully performing pulley stress and fatigue life analyses for the last nine years. PSTRESS was developed in 1984 and has been used to predict many failures before they actually happened and also as a valuable tool in forensic engineering. The finite element program was developed over two years ago. The design criteria and manufacturing notes presented herein are in present use at CDI. We make no claim that the information presented is exhaustive and sufficient. We do hope the information presented may be of help to initiate a program for better industrial norms. Furthermore, we would be pleased to participate in the development of better standards for our industry.
REFERENCES
British Standard BS 5400, 1980, "Steel concrete and composite bridges - Part 10- Code of practice for fatigue".
Bikon Locking Assemblies catalog 3A83, Bikon Corp.
Shigley, J. E., 1986, "Mechanical Engineering Design", McGraw-Hill.
Peterson, R. E., 1974, "Stress Concentration Factors", Wiley-lnterscience.
DeSalvo, G. J. and Gorman, R. W., 1989, ANSYS Users Manual for Revision 4.4", Swanson Analysis Systems, Inc., 1989, Houston, Pennsylvania, U.S.A.
Lindner, L, 1975, "Construction of a Conveyor Belt Pulley with the Aid of the TPS-10 Finite Element Program", Braunkohle 3, March 1975, pp. 81-97.
Lange, H., 1963, "Investigations on Stresses in Belt conveyor Pulleys", Doctoral Thesis, Technical University, Hannover.
Schmoltzi, W., 1974, "The Design of Conveyor Belt Pulleys with Continuous Shafts", Doctoral Thesis, Technical University, Hannover.
